We can use identities to help us solve trigonometric equations. Using a Double-Angle Formula we see that the equation sin(x) sin(2x) = 0 is equivalent to the equation . Factoring we see that solving this equation is equivalent to solving the two basic equations sin(x) = 0 and
We can use identities to help us solve trigonometric equations. Using a Double-Angle Formula we see that the equation sin(x) sin(2x) = 0 is equivalent to the equation . Factoring we see that solving this equation is equivalent to solving the two basic equations sin(x) = 0 and
Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter7: Analytic Trigonometry
Section7.5: More Trigonometric Equations
Problem 69E
Related questions
Question
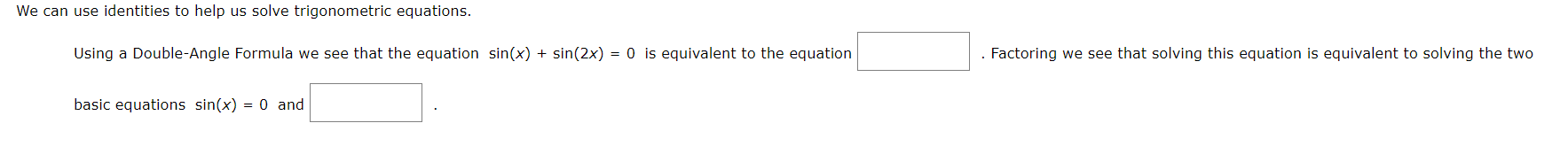
Transcribed Image Text:We can use identities to help us solve trigonometric equations.
Using a Double-Angle Formula we see that the equation sin(x) sin(2x) = 0 is equivalent to the equation
. Factoring we see that solving this equation is equivalent to solving the two
basic equations sin(x) = 0 and
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning