Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
where a and ß are positive and distinct real numbers. We handle two cases for the proof of Theorem. Firstly we consider a case such that m is even. We have from Eq.(8) a = 1+,ß = 1 + P. α

where a and ß are positive and distinct real numbers. We handle two cases for the proof of Theorem. Firstly we consider a case such that m is even. We have from Eq.(8) a = 1+,ß = 1 + P. α

Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter10: Sequences, Series, And Probability
Section10.4: Mathematical Induction
Problem 42E
See similar textbooks
icon
Related questions
Question

Show me the steps of determine yellow and inf is here

Theorem 6 Let {yn} be a positive solution of Eq. (8). Then Eq.(8) has no two periodic solution. Proof. We assume that there exist two periodic solution such that .* , a, B, a, B, ... where a and ß are positive and distinct real numbers. We handle two cases for the proof of Theorem. Firstly we consider a case such that m is even. We have from Eq.(8) a = 1+ B' 5,8=1+2. Hence we obtain that a? – - a - p = 0. So we get a = 1+/1+4p the other case such that m is odd. Now we apply Elsayed's new method for two periodic solution, see [16]. We have from Eq.(8) = j = B which is a trivial solution. Now we deal with 2 pB a =1+ Q2 pa = 1+ 4 Hence if we take a = Bn fornER- {0, 1,-1}. Therefore we obtain that Bn 1+ (9) %D pn 1+ (10) Thus, subtracting (10) from (9) gives the following (-) - р 1 —п° ,3 В (п — 1) n n2 From n + 1, we have -р (п? + п +1) n2 -р (п2 + п+1) n2 (11) Since B is real number, (11) is impossible for all real n and p > 0. This is a contradiction. So the proof is completed. .
Transcribed Image Text:Theorem 6 Let {yn} be a positive solution of Eq. (8). Then Eq.(8) has no two periodic solution. Proof. We assume that there exist two periodic solution such that .* , a, B, a, B, ... where a and ß are positive and distinct real numbers. We handle two cases for the proof of Theorem. Firstly we consider a case such that m is even. We have from Eq.(8) a = 1+ B' 5,8=1+2. Hence we obtain that a? – - a - p = 0. So we get a = 1+/1+4p the other case such that m is odd. Now we apply Elsayed's new method for two periodic solution, see [16]. We have from Eq.(8) = j = B which is a trivial solution. Now we deal with 2 pB a =1+ Q2 pa = 1+ 4 Hence if we take a = Bn fornER- {0, 1,-1}. Therefore we obtain that Bn 1+ (9) %D pn 1+ (10) Thus, subtracting (10) from (9) gives the following (-) - р 1 —п° ,3 В (п — 1) n n2 From n + 1, we have -р (п? + п +1) n2 -р (п2 + п+1) n2 (11) Since B is real number, (11) is impossible for all real n and p > 0. This is a contradiction. So the proof is completed. .
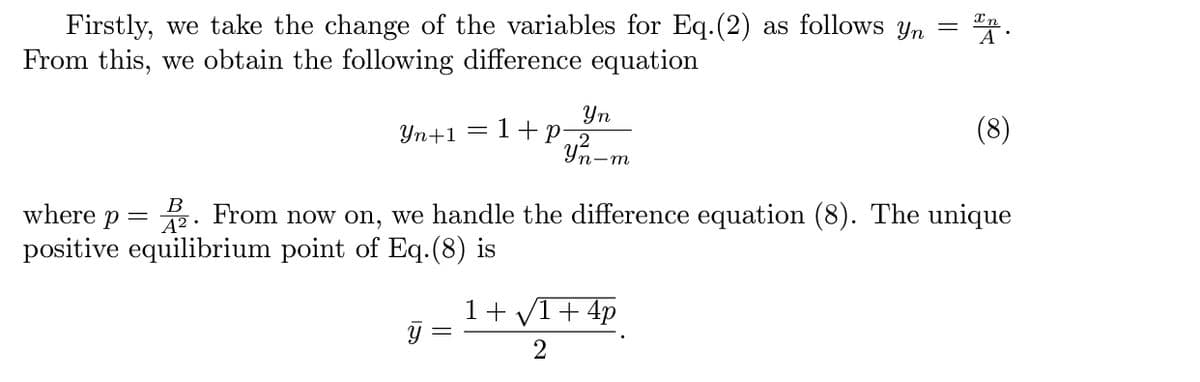
Firstly, we take the change of the variables for Eq.(2) as follows yn = From this, we obtain the following difference equation Yn 1+p Yn+1 = B where p = A² • From now on, we handle the difference equation (8). The unique positive equilibrium point of Eq.(8) is 1+ V1+ 4p
Transcribed Image Text:Firstly, we take the change of the variables for Eq.(2) as follows yn = From this, we obtain the following difference equation Yn 1+p Yn+1 = B where p = A² • From now on, we handle the difference equation (8). The unique positive equilibrium point of Eq.(8) is 1+ V1+ 4p
Expert Solution
steps

Step by step

Solved in 3 steps

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Elements Of Modern Algebra
Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,
Linear Algebra: A Modern Introduction
Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS