Suppose that o is an isomorphism from a group G onto a group G. Then 1. 6-1 is an isomorphism from G onto G. 2. G is Abelian if and only if G is Abelian. 3. G is cyclic if and only if G is cyclic. 4. If K is a subgroup of G, then 4(K) = {$(k) I k E K} is a subgroup of G. 5. If K is a subgroup of G, then o–1 (K) = {g E G I ¢(g) E K} is a subgroup of G. 6. 4(Z(G)) = Z(G).
Suppose that o is an isomorphism from a group G onto a group G. Then 1. 6-1 is an isomorphism from G onto G. 2. G is Abelian if and only if G is Abelian. 3. G is cyclic if and only if G is cyclic. 4. If K is a subgroup of G, then 4(K) = {$(k) I k E K} is a subgroup of G. 5. If K is a subgroup of G, then o–1 (K) = {g E G I ¢(g) E K} is a subgroup of G. 6. 4(Z(G)) = Z(G).
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter4: More On Groups
Section4.7: Direct Sums (optional)
Problem 10E: 10. Suppose that and are subgroups of the abelian group such that . If is a subgroup of such...
Related questions
Topic Video
Question
Prove property 1
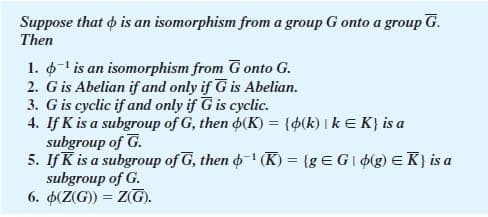
Transcribed Image Text:Suppose that o is an isomorphism from a group G onto a group G.
Then
1. 6-1 is an isomorphism from G onto G.
2. G is Abelian if and only if G is Abelian.
3. G is cyclic if and only if G is cyclic.
4. If K is a subgroup of G, then 4(K) = {$(k) I k E K} is a
subgroup of G.
5. If K is a subgroup of G, then o–1 (K) = {g E G I ¢(g) E K} is a
subgroup of G.
6. 4(Z(G)) = Z(G).
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,