Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
Chapter10: Analytic Geometry
Section10.1: The Rectangular Coordinate System
Problem 40E: Find the exact volume of the solid that results when the region bounded in quadrant I by the axes...
Related questions
Question
Find the positive constant A given that the volume of the solid bounded by the paraboloid, x2 + y2 +z = A in the first octant is 32π .
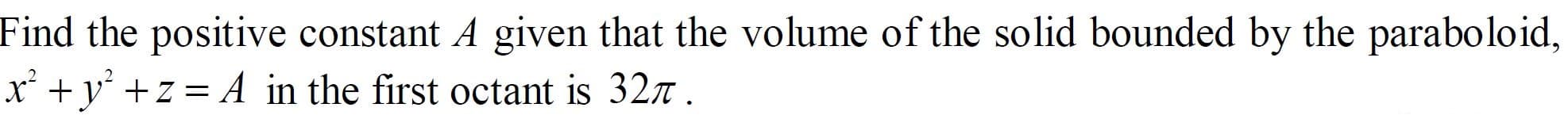
Transcribed Image Text:Find the positive constant A given that the volume of the solid bounded by the paraboloid,
x +y +z = A in the first octant is 327 .
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,