6. Find points P and Q on the parabola y = 1-x² so that AABC formed by the x-axis and the tan- gent lines at P and Q is an equilateral triangle. (Refer to Figure 1.) P Figure 1
6. Find points P and Q on the parabola y = 1-x² so that AABC formed by the x-axis and the tan- gent lines at P and Q is an equilateral triangle. (Refer to Figure 1.) P Figure 1
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter11: Topics From Analytic Geometry
Section11.3: Hyperbolas
Problem 24E
Related questions
Topic Video
Question
100%
Find points P and Q on the parabola y = 1−x^2 so that △ABC formed by the x−axis and the tangent lines at P and Q is an equilateral triangle.
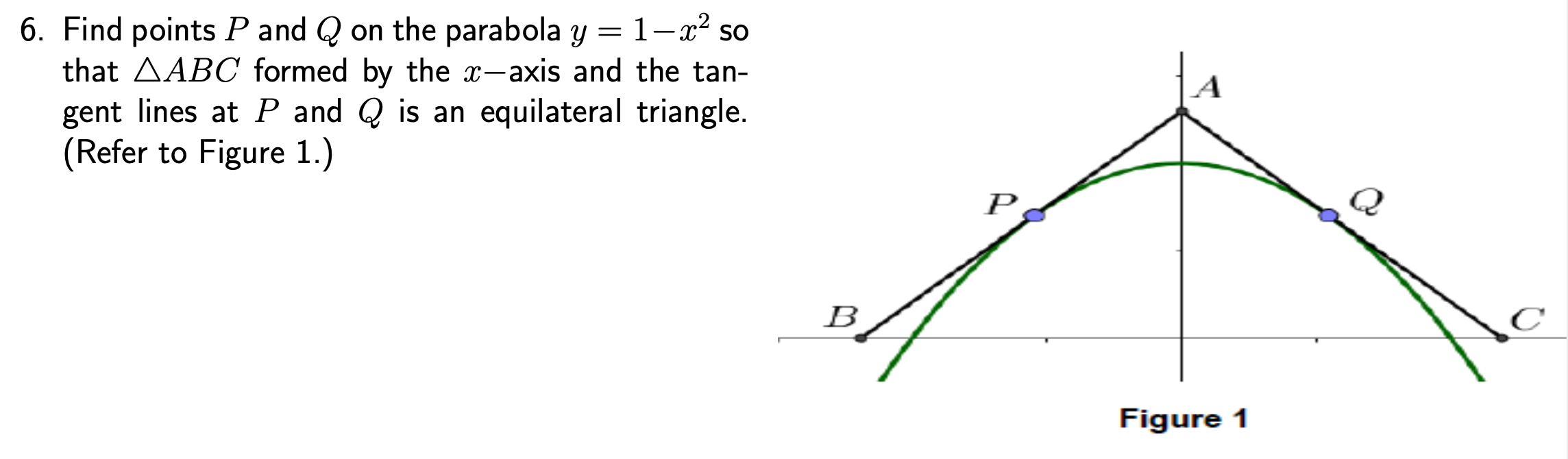
Transcribed Image Text:6. Find points P and Q on the parabola y = 1-x² so
that AABC formed by the x-axis and the tan-
gent lines at P and Q is an equilateral triangle.
(Refer to Figure 1.)
P
Figure 1
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 6 steps with 7 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage