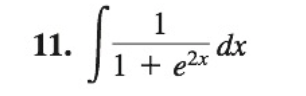Elementary Algebra 17th Edition
ISBN: 9780998625713
Author: Lynn Marecek, MaryAnne Anthony-Smith
Publisher: Lynn Marecek, MaryAnne Anthony-Smith
1 Foundations 2 Solving Linear Equations And Inequalities 3 Math Models 4 Graphs 5 Systems Of Linear Equations 6 Polynomials 7 Factoring 8 Rational Expressions And Equations 9 Roots And Radicals 10 Quadratic Equations Chapter6: Polynomials
6.1 Add And Subtract Polynomials 6.2 Use Multiplication Properties Of Exponents 6.3 Multiply Polynomials 6.4 Special Products 6.5 Divide Monomials 6.6 Divide Polynomials 6.7 Integer Exponents And Scientific Notation Chapter Questions Section6.2: Use Multiplication Properties Of Exponents
Problem 6.31TI: Simplify: (a) 63 (b) 151 (c) (37)2 (d) (0.43)2 Problem 6.32TI: Simplify: (a) 25 (b) 211 (c) (25)3 (d) (0.218)2 . Problem 6.33TI: Simplify: (a) (3)4 (b) 34 . Problem 6.34TI: Simplify: (a) (13)2 (b) 132 . Problem 6.35TI: Simplify: b9b8 . Problem 6.36TI: Simplify: x12x4 . Problem 6.37TI: Simplify: (a) 553 (b) 4949 . Problem 6.38TI: Simplify: (a) 7678 (b) 101010 Problem 6.39TI: Simplify: (a) p5p (b) y14y29 . Problem 6.40TI: Simplify: (a) zz7 (b) b15b34. Problem 6.41TI: Simplify: x6x4x8 . Problem 6.42TI: Simplify: b5b9b5 Problem 6.43TI: Simplify: (a) (b7)5 (b) (54)3 . Problem 6.44TI: Simplify: (a) (z6)9 (b) (37)7 Problem 6.45TI: Simplify: (a) (12y)2 (b) (2wx)5 . Problem 6.46TI: Simplify: (a) (5wx)3 (b) (3y)3 . Problem 6.47TI: Simplify: (a) (a4)5(a7)4 (b) (2c4d2)3 . Problem 6.48TI: Simplify: (a) (3x6y7)4 (b) (q4)5(q3)3 . Problem 6.49TI: Simplify: (a) (5n)2(3n10) (b) (c4d2)5(3cd5)4 . Problem 6.50TI: Simplify: (a) (a3b2)6(4ab3)4 (b) (2x)3(5x7) . Problem 6.51TI: Multiply: (5y7)(7y4) . Problem 6.52TI: Multiply: (6b4)(9b5) . Problem 6.53TI: Multiply: (25a4b3)(15ab3) . Problem 6.54TI: Multiply: (23r5s)(12r6s7) . Problem 88E: In the following exercises, simplify each expression with exponents. 88. (a) 35 (b) 91 (c) (13)2 (d)... Problem 89E: In the following exercises, simplify each expression with exponents. 89. (a) 104 (b) 171 (c) (29)2... Problem 90E: In the following exercises, simplify each expression with exponents. 90. (a) 26 (b) 141 (c) (25)3... Problem 91E: In the following exercises, simplify each expression with exponents. 91. (a) 83 (b) 81 (c) (34)3 (d)... Problem 92E: In the following exercises, simplify each expression with exponents. 92. (a) (6)4 (b) 64 Problem 93E: In the following exercises, simplify each expression with exponents. 93. (a) (2)6 (b) 26 Problem 94E: In the following exercises, simplify each expression with exponents. 94. (a) (14)4 (b) (14)4 Problem 95E: In the following exercises, simplify each expression with exponents. 95. (a) (23)2 (b) (23)2 Problem 96E: In the following exercises, simplify each expression with exponents. 96. (a) 0.52 (b) (0.5)2 Problem 97E: In the following exercises, simplify each expression with exponents. 97. (a) 0.14 (b) (0.1)4 Problem 98E: In the following exercises, simplify each expression using the Product Property for Exponents. 98.... Problem 99E: In the following exercises, simplify each expression using the Product Property for Exponents. 99.... Problem 100E: In the following exercises, simplify each expression using the Product Property for Exponents. 100.... Problem 101E: In the following exercises, simplify each expression using the Product Property for Exponents. 101.... Problem 102E: In the following exercises, simplify each expression using the Product Property for Exponents. 102.... Problem 103E: In the following exercises, simplify each expression using the Product Property for Exponents. 103.... Problem 104E: In the following exercises, simplify each expression using the Product Property for Exponents. 104.... Problem 105E: In the following exercises, simplify each expression using the Product Property for Exponents. 105.... Problem 106E: In the following exercises, simplify each expression using the Product Property for Exponents. 106.... Problem 107E: In the following exercises, simplify each expression using the Product Property for Exponents. 107.... Problem 108E: In the following exercises, simplify each expression using the Product Property for Exponents. 108.... Problem 109E: In the following exercises, simplify each expression using the Product Property for Exponents. 109.... Problem 110E: In the following exercises, simplify each expression using the Product Property for Exponents. 110.... Problem 111E: In the following exercises, simplify each expression using the Product Property for Exponents. 111.... Problem 112E: In the following exercises, simplify each expression using the Product Property for Exponents. 112.... Problem 113E: In the following exercises, simplify each expression using the Product Property for Exponents. 113.... Problem 114E: In the following exercises, simplify each expression using the Product Property for Exponents. 114.... Problem 115E: In the following exercises, simplify each expression using the Product Property for Exponents. 115.... Problem 116E: In the following exercises, simplify each expression using the Product Property for Exponents. 116.... Problem 117E: In the following exercises, simplify each expression using the Product Property for Exponents. 117.... Problem 118E: In the following exercises, simplify each expression using the Product Property for Exponents. 118.... Problem 119E: In the following exercises, simplify each expression using the Product Property for Exponents. 119.... Problem 120E: In the following exercises, simplify each expression using the Product Property for Exponents. 120.... Problem 121E: In the following exercises, simplify each expression using the Product Property for Exponents. 121.... Problem 122E: In the following exercises, simplify each expression. 122. (a) (y2)4(y3)2 (b) (10a2b)3 Problem 123E: In the following exercises, simplify each expression. 123. (a) (w4)3(w5)2 (b) (2xy4)5 Problem 124E: In the following exercises, simplify each expression. 124. (a) (2r3s2)4 (b) (m5)3(m9)4 Problem 125E: In the following exercises, simplify each expression. 125. (a) (10q2p4)3 (b) (n3)10(n5)2 Problem 126E: In the following exercises, simplify each expression. 126. (a) (3x)2(5x) (b) (5t2)3(3t)2 Problem 127E: In the following exercises, simplify each expression. 127. (a) (2y)3(6y) (b) (10k4)3(5k6)2 Problem 128E: In the following exercises, simplify each expression. 128. (a) (5a)2(2a)3 (b) (12y2)3(23y)2 Problem 129E: In the following exercises, simplify each expression. 129. (a) (4b)2(3b)3 (b) (12j2)5(25j3)2 Problem 130E: In the following exercises, simplify each expression. 130. (a) (25x2y)3 (b) (89xy4)2 Problem 131E: In the following exercises, simplify each expression. 131. (a) (2r2)3(4r)2 (b) (3x3)3(x5)4 Problem 132E: In the following exercises, simplify each expression. 132. (a) (m2n)2(2mn5)4 (b) (3pq4)2(6p6q)2 Problem 133E: In the following exercises, multiply the monomials. 133. (6y7)(3y4) Problem 134E: In the following exercises, multiply the monomials. 134. (10x5)(3x3) Problem 135E: In the following exercises, multiply the monomials. 135. (8u6)(9u) Problem 136E: In the following exercises, multiply the monomials. 136. (6c4)(12c) Problem 137E: In the following exercises, multiply the monomials. 137. (15f8)(20f3) Problem 138E: In the following exercises, multiply the monomials. 138. (14d5)(36d2) Problem 139E: In the following exercises, multiply the monomials. 139. (4a3b)(9a2b6) Problem 140E: In the following exercises, multiply the monomials. 140. (6m4n2)(7mn5) Problem 141E: In the following exercises, multiply the monomials. 141. (47rs2)(14rs3) Problem 142E: In the following exercises, multiply the monomials. 142. (58x3y)(24x5y) Problem 143E: In the following exercises, multiply the monomials. 143. (23x2y)(34xy2) Problem 144E: In the following exercises, multiply the monomials. 144. (35m3n2)(59m2n3) Problem 145E: In the following exercises, multiply the monomials. 145. (x2)4(x3)2 Problem 146E: In the following exercises, multiply the monomials. 146. (y4)3(y5)2 Problem 147E: In the following exercises, multiply the monomials. 147. (a2)6(a3)8 Problem 148E: In the following exercises, multiply the monomials. 148. (b7)5(b2)6 Problem 149E: In the following exercises, simplify each expression. 149. (2m6)3 Problem 150E: In the following exercises, simplify each expression. 150. (3y2)4 Problem 151E: In the following exercises, simplify each expression. 151. (10x2y)3 Problem 152E: In the following exercises, simplify each expression. 152. (2mn4)5 Problem 153E: In the following exercises, simplify each expression. 153. (2a3b2)4 Problem 154E: In the following exercises, simplify each expression. 154. (10u2v4)3 Problem 155E: In the following exercises, simplify each expression. 155. (23x2y)3 Problem 156E: In the following exercises, simplify each expression. 156. (79pq4)2 Problem 157E: In the following exercises, simplify each expression. 157. (8a3)2(2a)4 Problem 158E: In the following exercises, simplify each expression. 158. (5r2)3(3r)2 Problem 159E: In the following exercises, simplify each expression. 159. (10p4)3(5p6)2 Problem 160E: In the following exercises, simplify each expression. 160. (4x3)3(2x5)4 Problem 161E: In the following exercises, simplify each expression. 161. (12x2y3)4 (4x5y3)2 Problem 162E: In the following exercises, simplify each expression. 162. (13m3n2)4(9m8n3)2 Problem 163E: In the following exercises, simplify each expression. 163. (3m2n)2(2mn5)4 Problem 164E: In the following exercises, simplify each expression. 164. (2pq4)(5p6q)2 Problem 165E: Email Kate emails a flyer to ten of her friends and tells them to forward it to ten of their... Problem 166E: Salary Jamal’s boss gives him a 3% raise every year on his birthday. This means that each year,... Problem 167E: Clearance A department store is clearing out merchandise in order to make room for new inventory.... Problem 168E: Depreciation Once a new car is driven away from the dealer, it begins to lose value. Each year, a... Problem 169E: Use the Product Property for Exponents to explain why xx=x2 . Problem 170E: Explain why 53=(5)3 but 54(5)4 . Problem 171E: Jorge thinks (12)2 is 1. What is wrong with his reasoning? Problem 172E: Explain why x3x5 is x8 , and not x15 . Problem 6.46TI: Simplify: (a) (5wx)3 (b) (3y)3 .
Related questions
In Exercises 11 and 12, use a table of integrals with forms involving eu to find the indefinite integral.
Transcribed Image Text: 1
dx
1 + e2x
11.
With differentiation, one of the major concepts of calculus. Integration involves the calculation of an integral, which is useful to find many quantities such as areas, volumes, and displacement.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images