20 kN/m B 150 kN 4 m |-1.5 m-1.5 m- 5 m El = constant E= 200 GPa I= 500 (106) mm+ FIG. P7.41, P7.42
20 kN/m B 150 kN 4 m |-1.5 m-1.5 m- 5 m El = constant E= 200 GPa I= 500 (106) mm+ FIG. P7.41, P7.42
Chapter2: Loads On Structures
Section: Chapter Questions
Problem 1P
Related questions
Question
Use the virtual work method to determine the vertical deflection at joint B of the frame shown in Fig. P7.41.
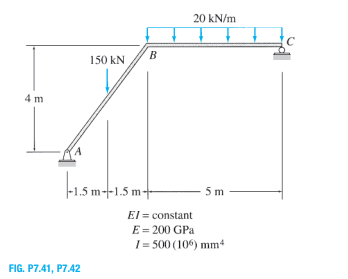
Transcribed Image Text:20 kN/m
B
150 kN
4 m
|-1.5 m-1.5 m-
5 m
El = constant
E= 200 GPa
I= 500 (106) mm+
FIG. P7.41, P7.42
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Recommended textbooks for you


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:
9780134610672
Author:
Russell C. Hibbeler
Publisher:
PEARSON

Principles of Foundation Engineering (MindTap Cou…
Civil Engineering
ISBN:
9781337705028
Author:
Braja M. Das, Nagaratnam Sivakugan
Publisher:
Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:
9780073398006
Author:
Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:
McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:
9781305156241
Author:
Garber, Nicholas J.
Publisher:
Cengage Learning