Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Evaluate the integral #22
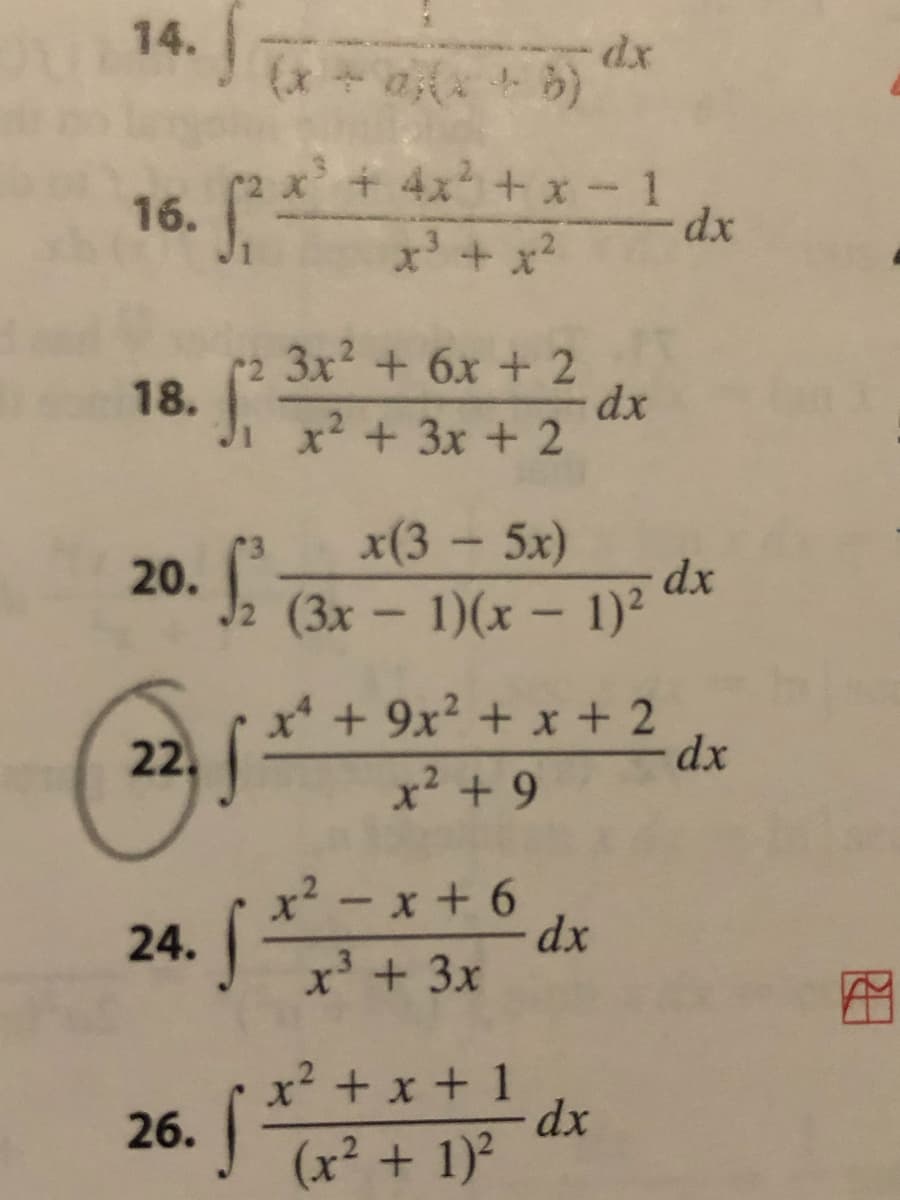
Transcribed Image Text:20. J. (3x - 1)(x - 1)2 dx
14.
+4x + x- 1
16.
x' + x'
3x2 + 6x + 2
dx
x² +3x + 2
18.
x(3 - 5x)
20.
J2 (3x- 1)(x-
dx
1)2
x* + 9x? + x + 2
22.
dx
x² + 9
x - x + 6
dx
24.
x³ + 3x
x² + x + 1
dx
26.
(x² + 1)?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
Expert Answers to Latest Homework Questions
Q: Jennifer owns a construction company that builds custom houses. She hired Steve, an out-of-work…
Q: Jennifer owns a construction company that builds custom houses. She hired Steve, an out-of-work…
Q: Sue applied for a position as a receptionist at Bethany’s brokerage. Bethany, who was busy with…
Q: Can you provide a mechanism for this reaction? I’d also like maybe a sentence or two explaining each…
Q: A person who acts with the apparent authority of a principal may have created a[n] _________________…
Q: The current spot rate between the euro and dollar is €1.1023/$. The annual inflation rate in the U.S…
Q: The current spot rate between the pound and dollar is £.7562/$. The expected inflation rate in the…
Q: A company manufactures two types of electric hedge trimmers, one of which is cordless. The cord-type…
Q: a. Apex Motors manufactures luxury cars and sport-utility vehicles. The most likely customers are…
Q: Bill, a broker, had no authorization from Larry, a property owner, to lease some property that Larry…
Q: A document sometimes used to establish an agency relationship is known as:
Group of answer choices…
Q: Find the concentration of Ba2+ in a 0.100 M (CH 3 ) 4 NIO3 solution saturated with Ba(IO3 ) 2 .…
Q: 1
a). Find the concentration of hydroxide ion in 0.10 M NaClO 4 saturated with Mn(OH)2(Ksp = 1.6 x…
Q: The manager of Bob's Yacht Sales has approved your application for credit. The maximum payment she…
Q: Please don't provide handwritten solution ....
Q: 46. The tabulated data were collected for this reaction:
CH3Cl(g) + 3 Cl2(g)
CC14(g) + 3 HCl(g)…
Q: Predict the structure of the product of each of these reactions. If no reaction occurs write NR…
Q: Select all that applies
Q: phosphofructokinase reaction of
Fructose-2,6-bisphosphate is a regulator of both glycolysis and…
Q: Consider the following non-homogeneous first-order differential equation,
where y
=
dy
.
dt
Ty' + y…
Q: Homo floresiensis
describe the fossil/ DNA etc. and where it comes from.
Describe what makes this…