Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Evaluate the integral #22
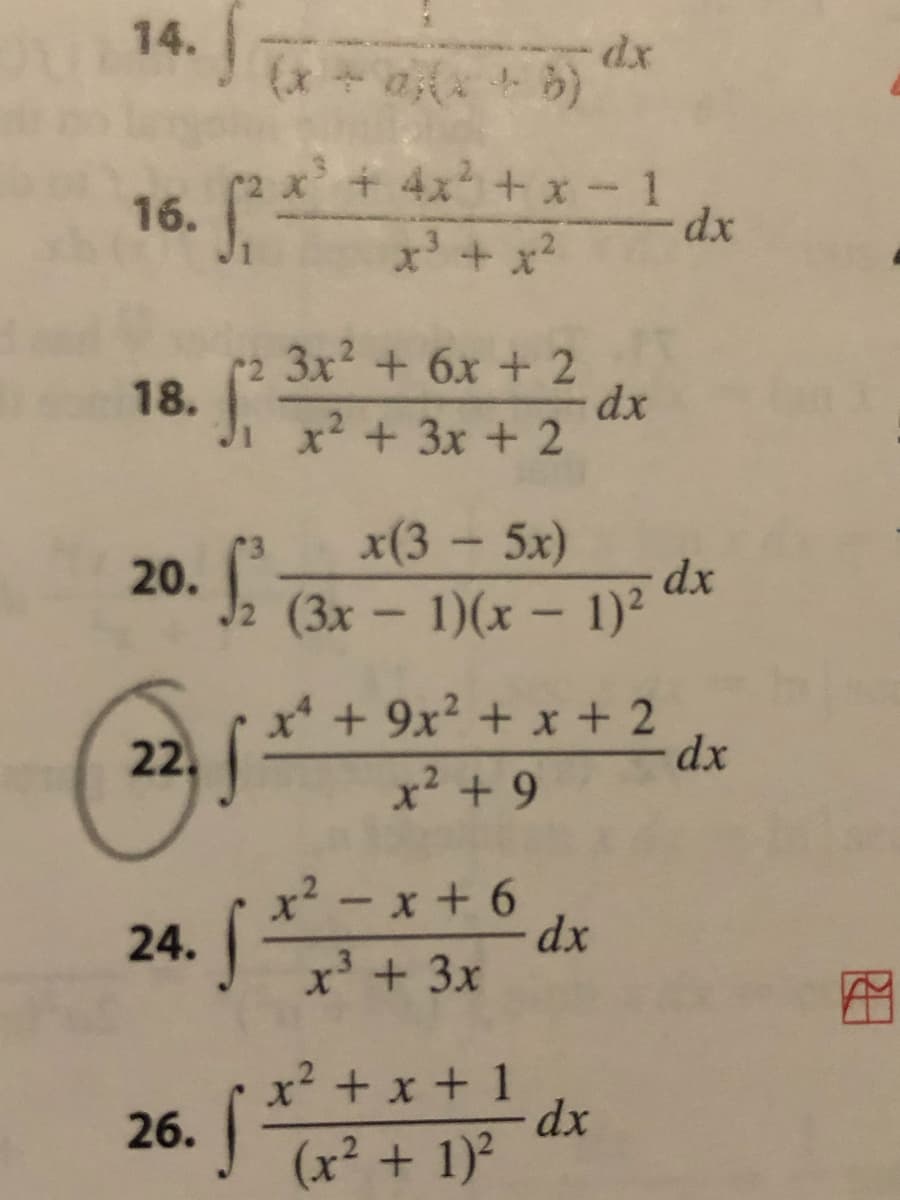
Transcribed Image Text:20. J. (3x - 1)(x - 1)2 dx
14.
+4x + x- 1
16.
x' + x'
3x2 + 6x + 2
dx
x² +3x + 2
18.
x(3 - 5x)
20.
J2 (3x- 1)(x-
dx
1)2
x* + 9x? + x + 2
22.
dx
x² + 9
x - x + 6
dx
24.
x³ + 3x
x² + x + 1
dx
26.
(x² + 1)?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
Expert Answers to Latest Homework Questions
Q: Dion is developing an application that will allow users to create their own passwords. He then needs…
Q: Suppose yao + a₁yt-1 + ut, and u₁ = put-1 + et and et is serially uncorrelated with es
where st.
(a)…
Q: Penelope has just been hired as a cybersecurity manager for an organization. She has done an initial…
Q: Penelope has just been hired as a cybersecurity manager for an organization. She has done an initial…
Q: Hattie has just been promoted to the cybersecurity team within her organization. Her new manager…
Q: Alisi, a cybersecurity manager, has found that a former employee was engaging in illegal activities…
Q: Faruq is an administrator for a large movie production studio. He has just been sent the mastered…
Q: Using a graph, discuss how the elasticity of demand influences the incidence of a tax
Q: Justin has just received a report from a security consultant with a line item stating that it is…
Q: Redistributive expenditure can take the form of direct cash transfers (grants) and/or inkind…
Q: A R1000 tax payable by all adults could be viewed as both a proportional tax and a regressive tax.…
Q: In Exercises 1-4, show that A and B are not similar matrices.
1. A =
B
1
*-69-67
=
3
4
2. A =
2
B =…
Q: Veeti is creating a policy document defining the roles of various positions within the IT…
Q: Karin has just finished crafting a policy that describes and defines what users are allowed to do on…
Q: Which of the following is not a term used to describe how computer systems impose standard access…
Q: Hi please assist with the 3 questions attached
Q: Vicente manages the AAA server at his organization. He knows that the server plays a key role in…
Q: Bartolo sees a notification from a security device on the perimeter of the network that ICMP echo…
Q: Please help me determine wheather the following types of south african grasses are increasers (what…
Q: Bartolo sees a notification from a security device on the perimeter of the network that ICMP echo…
Q: Ramsey is working on migrating data to a cloud service provider. As part of the service design, he…