Calculus: Early Transcendentals
8th Edition
ISBN:9781285741550
Author:James Stewart
Publisher:James Stewart
Chapter1: Functions And Models
Section: Chapter Questions
Problem 1RCC: (a) What is a function? What are its domain and range? (b) What is the graph of a function? (c) How...
Related questions
Question
Evaluate the integral #22
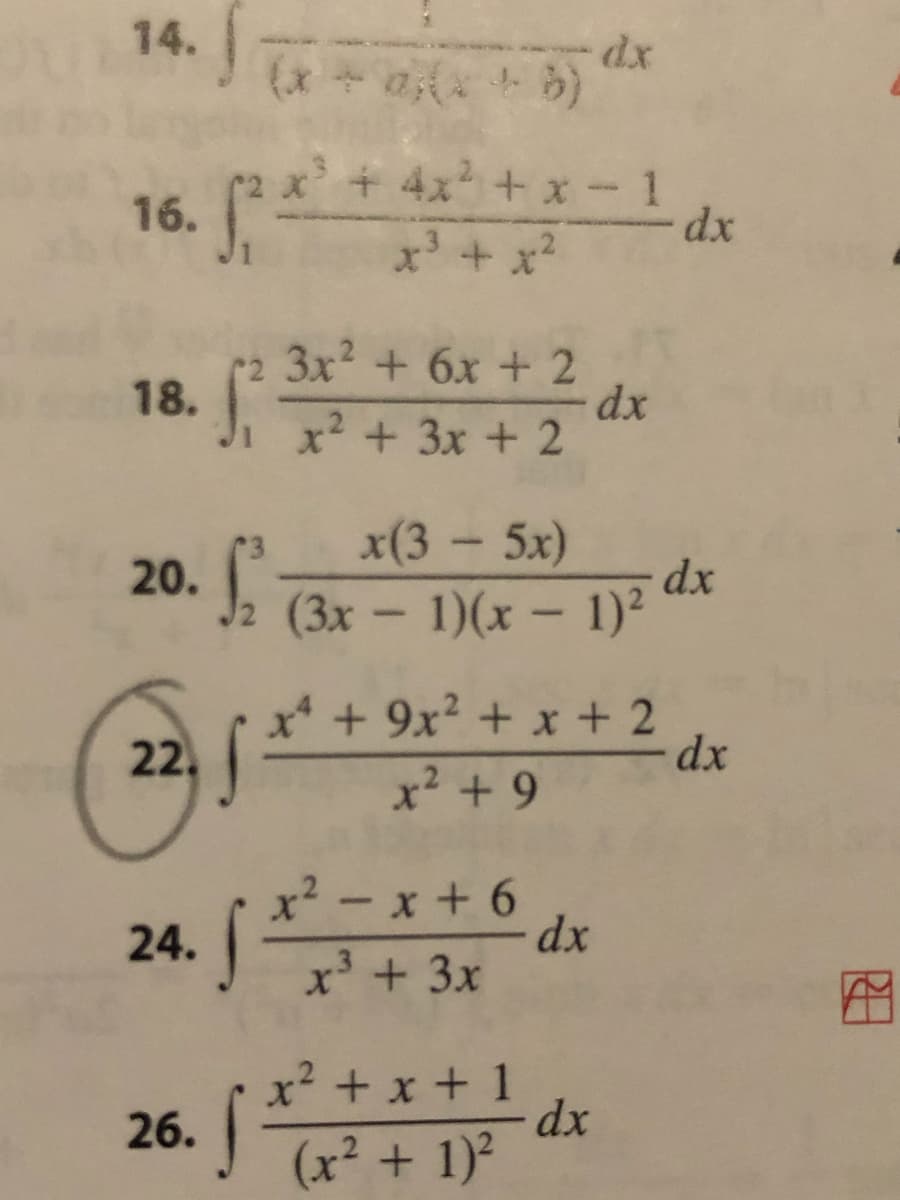
Transcribed Image Text:20. J. (3x - 1)(x - 1)2 dx
14.
+4x + x- 1
16.
x' + x'
3x2 + 6x + 2
dx
x² +3x + 2
18.
x(3 - 5x)
20.
J2 (3x- 1)(x-
dx
1)2
x* + 9x? + x + 2
22.
dx
x² + 9
x - x + 6
dx
24.
x³ + 3x
x² + x + 1
dx
26.
(x² + 1)?
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781285741550
Author:
James Stewart
Publisher:
Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:
9780134438986
Author:
Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:
PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:
9780134763644
Author:
William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:
PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:
9781319050740
Author:
Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:
W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:
9781337552516
Author:
Ron Larson, Bruce H. Edwards
Publisher:
Cengage Learning
Expert Answers to Latest Homework Questions
Q: When doctors prescribe L-dopa to Parkinson's patients, the typical initial prescription is 1.5 grams…
Q: The rate at which a particular medication leaves an individual's bloodstream is proportional to the…
Q: th
The term of a sequence is given. Find the indicated term. Express the term as a simplified…
Q: Find the sixth term of the binomial expansion.
(p+q)11
The sixth term of the expansion is
×
Q: The general solution of the differential equation dy_Y, where x = 0, is a family of which of the…
Q: A 3-foot-tall dog cases a 4-foot shadow at the same time a cat casts a one foot shadow. How tall is…
Q: Determine the value of k that will make y = 2cos(2x) a solution to ky - y" = y.
Ok = 5
Ok=0
Ok = -3…
Q: Sales transactions are recorded in the general journal by debiting Accounts Receivable and crediting…
Q: Based on the graph of the general solution to the differential equation
dy=2x-
The slopes along the…
Q: A heat source is applied to a metal surface, causing the temperature of the metal to increase with…
Q: Select the general solution to x-
I. 21nly + 3y In|x| + C
II.
12+3y
In
|= In|x|+C
01
O ll
O Both
○…
Q: Just the section 3 only
Q: Just do the section 2 only
Q: Expectations: 1. Normalize the data, provide rationale for the tables you create, create the…
Q: x=5e' and y=e' +3
Part 1 of 2
(a) Eliminate the parameter and write an equation in rectangular…
Q: Jade Company uses the perpetual inventory system. It bought merchandise from Lilac Company. After…
Q: Question 9 (4 points)
Differenciate: y=
·(32³ - 62²)s
= 30(x²-1)(3x²-6x)4
•
Oy=24(x-1)(3x²-6x)4
y' =…
Q: Determine the eccentricity of the ellipse. Express numbers in simplest form using integers,…
Q: Question 7 (5 points)
For
y =
=20x4 - 16x3 - 10x + 20, find
d³y
dx3
240x2-32x
73
82,425
C
480x 96…
Q: Azure Company sold merchandise on account to P. Parker for $150. Which of the following journal…
Q: Question 6 (5 points)
r – 52+7
Differentiate: y =
x4 - 3
5
บ
18
--
-2x5 - 15x4-28x3+6x+15
(4-3)2…