Find the volume of the solid that lies above the xy-plane and is bounded by the cylinder x^2 + y^2 =1 and the plane x +y + z = 2 Find the volume of the solid that lies above the xy-plane and is bounded by the cylinderx² + y² = 1 and the plane x + y +z = 2.%3D

Answered: Find the volume of the solid that lies…

Find the volume of the solid that lies above the xy-plane and is bounded by the cylinder x^2 + y^2 =1 and the plane x +y + z = 2

Elementary Geometry For College Students, 7e

7th Edition

ISBN:9781337614085

Author:Alexander, Daniel C.; Koeberlein, Geralyn M.

Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.

Chapter10: Analytic Geometry

Section10.1: The Rectangular Coordinate System

Problem 40E: Find the exact volume of the solid that results when the region bounded in quadrant I by the axes...

See similar textbooks

Related questions

Q: Find the volume of the solid generated by revolving the region 2 bounded by y + 2v2x = (x+ v2)´and x…

Q: Find the volume of the 'cover' that is bounded by 52 < x2 + y2 + z² < 7² and the upper cone z² = 4x2…

A: Given 52≤x2+y2+z2≤72 ,z2=4x2+4y2

Q: Find the volume of the solid bounded above by f(x,y) = 5x², below by the xy-plane and the sides by y…

Q: Find the volume of the solid of revolution formed by revolving the region bounded by y = f(x) = 2x -…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

Q: Find the volume of the solid bounded by the plane 2x + 8y + 5z = 2 in the first octant. Leave your…

A: Equation of plane, 2x + 8y + 5z =2

Q: Find the volume of the solid that is bounded by the surfaces z = = 92 - x2 - y2 in the first octant.…

A: 0≤ z ≤ 81-x2-y2z=0x2+y2=920≤y≤81-x20≤x≤9

Q: Find the volume of the solid that is bounded by the surfaces z = 192 - x2 - y², z = 0, x = 0, y = 0…

A: Find the volume of the solid.

Q: Find the volume of the solid generated when the region bounded by x = 2y², y-axis, the lines y = 3…

Q: find the volume of the solid bounded by y=2x+1,y=3and x=4 about line y=10usingthe cylindrical shell…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

Q: Find the volume of the solid bounded by the elliptic cylinder 4x2 + z2 = 4 and the planes y = 0 and…

A: According to the given information, it is required to find the volume of the solid bounded by…

Q: Find the volume of the solid bounded above by the z=2−x plane and below by the x=4−y^2 curve, in the…

Q: Find the volume of the solid obtained by rotating the region bounded by y = x² + 2 and y = 4 - x²…

A: Solution:-

Q: Find the volume of the solid generated by revolving the finite region bounded by the curves y= x^2+1…

A: Consider the provided question, We have to find the volume of solid generated by revolving the…

Q: Find the volume of the solid bounded above by f(x,y) = 8x², below by the xy-plane and the sides by y…

A: Volume

Q: Find the volume of the solid generated when the region bounded by y = 4x and y = 16VX is revolved…

Q: Find the volume of the region under the surface z and above the triangle in the xy-plane with 1+ x²…

A: We have to find the volume of the region under the surface.

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

Q: Calculate the volume of the solid bounded by cone z2=x2+y2 and cylinder 4=x2+y2.

Q: Find the volume of the solid obtained by rotating the region bounded by the given curves about the…

A: The region to be rotated and the limits will be as follows.

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

Q: Find the volume of the solid bounded above by f(x,y) = 3x2, below by the xy-plane and the sides by y…

A: Let's find.

Q: Find the volume of the solid generated by revolving the region bounded by curves and lines in y =2x,…

Q: Find the volume of the solid generated when the area bounded by the given curves and lines is…

A: You have posted multiple questions. As per the instruction, we will be answering only the first…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

Q: Find the volume of the solid with the order dzdydx bounded by x2 + y2 = 4 and the planes x + z=2,…

Q: Find the volume of the region bounded by: y = x2 +1 y 2 that is rotated about the liney

Q: Find the volume of the solid generated by revolving the region bounded by y = 2x – x² and y = x…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

A: according to given conditions

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

A: Consider the given equations: The region is bounded by 0 to 6. The volume of the enclosed region…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

A: Given y=x And y=3 , x=0 Line y=7

Q: Calculate the volume of the region bounded by the spherex + y² + z² = 9 from above and by the cone…

Q: Find the volume of the solid bounded above by f(x,y) = 7x2, below by the xy-plane and the sides by y…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

Q: Find the volume of the solid bounded by z = 9 − x2, z= 0, y= 0, y = 2x.

Q: Find the volume of the solid bounded above by f(x,y) = 4x?, below by the xy-plane and the sides by y…

A: We will find out the required volume.

Q: Find the volume of the solid obtained by rotating the region bounded by the given curves about the…

A: Plot the curves to find the area of the bounded region formed by the curves.

Q: Find the volume of the solid generated by revolving the region bounded by y=sqrtx and the lines y=2…

A: The graph of the region is shown below:

Q: Find the volume of the solid generated by revolving about the y-axis and the region is bounded by x…

Q: Find the volume of the solid generated of the area bounded by y = x², y + 2x = 8 and y = 0, rotat…

Q: Determine the volume of the solid obtained by rotating the region bounded by y= 2x2 and y = x³ about…

Q: Find the volume of the solid generated by revolving the region bounded by the graphs of the…

A: To determine: The volume of the solid generated by revolving the region bounded by the graph of the…

Q: Find the volume of the solid that is bounded by the surfaces z = 92 - x2 - y2 in the first octant.…

Q: Find the volume of the solid generated by revolving the region. 2 bounded by y + 2v2x = (x+ v2)´and…

A: Simplify the given equations to obtain the expression of y. Use the algebraic identity…

Q: Find the volume of the solid generated by revolving the region bounded by y = x2 - 2x + 2, x = 0, x…

A: Given: The region is bounded by the curves : y=x2-2x+2, x=0, x=1 and y=1 We have to find the volume…

Q: Find the volume of the solid in the first octant bounded by the parabolic cylinder z= 25 - x and the…

A: Since we are considering only in the first octant so lower limit of both x and y will be zero.…

Question

Find the volume of the solid that lies above the xy-plane and is bounded by the cylinder x^2 + y^2 =1 and the plane x +y + z = 2

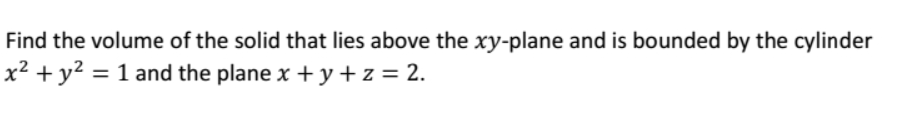
Find the volume of the solid that lies above the xy-plane and is bounded by the cylinder
x² + y² = 1 and the plane x + y +z = 2.
%3D

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Step 3

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 3 steps

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Triple Integral$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.