Trigonometry (MindTap Course List)
10th Edition
ISBN:9781337278461
Author:Ron Larson
Publisher:Ron Larson
Chapter2: Analytic Trigonometry
Section2.3: Solving Trigonometric Equations
Problem 9ECP: Solve 4tan2x+5tanx6=0.
Related questions
Question
Use the Taylor Series in Table 11.5 to find the first four nonzero terms of the Taylor Series for the following functions centered at 0.
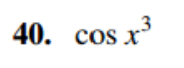
Transcribed Image Text:3
40. cos x

Transcribed Image Text:Table 11.5 asserts, without proof, that
in several cases, the Taylor series for
f converges to f at the endpoints of
the interval of convergence. Proving
Table 11.5
1
= 1 + x + x² +
1- x
+ x* +
Ert, for |x| < 1
... -
k=0
convergence at the endpoints generally
requires advanced techniques. It may also
be done using the following theorem:
Suppose the Taylor series for f
centered at 0 converges to f on the
interval (-R, R). If the series converges
at x = R, then it converges to lim f(x).
1
= 1 - x + x² .
- E(-1)x*, for [x| < 1
- ..·+ (-1)*x* + • · · =
|
1 + x
k=0
for |x| < 0
k!
e = 1 + x +
+
+
+
... -
2!
k!
k=0
(-1)*x*+1
(2k + 1)!
(-1)*x*+1
(2k + 1)!
sin x = x –
+
for x < 0
+... =
If the series converges at x = -R, then it
3!
5!
k=0
converges to lim f(x).
x--R+
(-1)*x*
Σ
(2k)!
(-1)* x*
2k
x2
+
2!
00
For example, this theorem would
for |x| < ∞
cos x = 1
+...=
allow us to conclude that the series for
4!
(2k)!
k=0
In (1 + x) converges to In 2 at x = 1.
x?
In (1 + x) = x -
(-1)*+1 *
+
(-1)*+'*
Σ
for -1 < x< 1
+... =
3
k
k=1
-In (1 – x) :
x?
= x +
+
+
k
for -1 < x < 1
3
k=1
(-1)*x*+1
(-1)* x*+1
-1
tan
Σ
2k + 1
for |x| < 1
n¯'x = x -
+
+...=
3
2k + 1
k=0
x2k+1
Σ
k=o(2k + 1)!’
x2k+1
sinh x = x +
3!
for x < 0
+...=
5!
(2k + 1)!
cosh x = 1 +
+
4!
Σ
for x < 0
+... =
(2k)!
(2k)!
k=0
p(p – 1)(p – 2) · ·· (p – k + 1) (P) :
As noted in Theorem 11.6, the binomial
series may converge to (1 + x)® at
x = ±1, depending on the value of p.
(2)
...
(1 + x)" =
Σ
x*, for x < 1 and
= 1
k!
=0
+
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781305652224
Author:
Charles P. McKeague, Mark D. Turner
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,