45°2460°Right-Triangle-Based Definitions of Trigonometric FunctionsLet A represent any acute angle in standard position.sin Aside opposite Ahypotenusese 4--=r hypotenusex side adjacent to Ar hypotenusey side opposite AhypotenuseCOSA =-=sec A =-=xside adjacent to Atan Acot A = x = side adjacent to Ax-sideadjacenttoA,y side opposite AFunction Values of Special Anglessin θ | cos θ | tan θ | cot θsec θcse θ30°阪|1|阪V360°

Question

Asked Jan 29, 2019

5 views

Find the exact values for the unknown sides. You can find the sides in any order.

Use the green box and the yellow table to help.

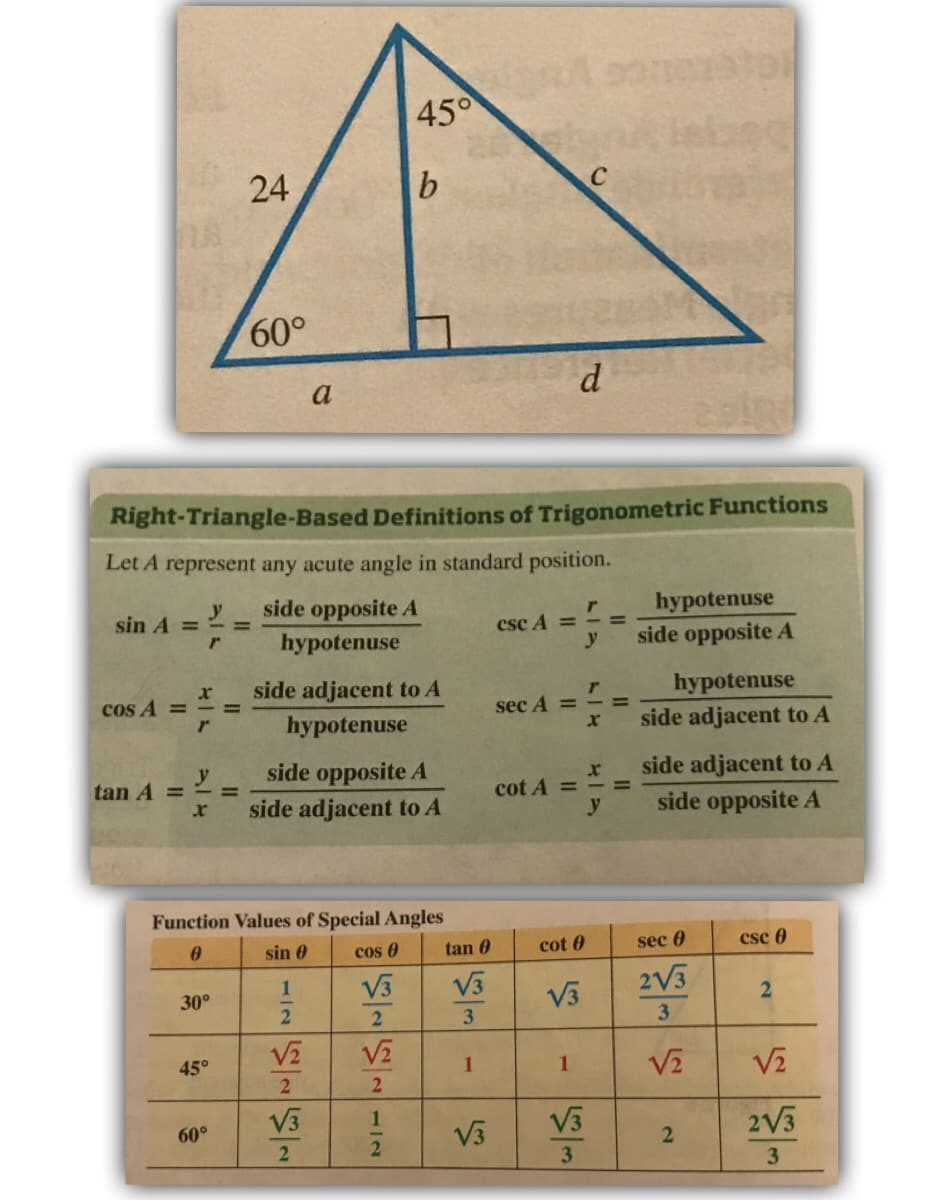
45°
24
60°
Right-Triangle-Based Definitions of Trigonometric Functions
Let A represent any acute angle in standard position.
sin A
side opposite A
hypotenuse
se 4-
-=
r hypotenuse
x side adjacent to A
r hypotenuse
y side opposite A
hypotenuse
COSA =-=
sec A =-=
x
side adjacent to A
tan A
cot A = x = side adjacent to A
x-sideadjacenttoA,
y side opposite A
Function Values of Special Angles
sin θ | cos θ | tan θ | cot θ
sec θ
cse θ
30°
阪|1|阪
V3
60° — Image Transcription
45° 24 60° Right-Triangle-Based Definitions of Trigonometric Functions Let A represent any acute angle in standard position. sin A side opposite A hypotenuse se 4- -= r hypotenuse x side adjacent to A r hypotenuse y side opposite A hypotenuse COSA =-= sec A =-= x side adjacent to A tan A cot A = x = side adjacent to A x-sideadjacenttoA, y side opposite A Function Values of Special Angles sin θ | cos θ | tan θ | cot θ sec θ cse θ 30° 阪|1|阪 V3 60°

Expert Answer

Step 1

The diagram is on the board . First we use sin 60 = a/24, and sol...

Want to see the full answer?

See Solution

Check out a sample Q&A here.

Want to see this answer and more?

Solutions are written by subject experts who are available 24/7. Questions are typically answered within 1 hour.*

See Solution

*Response times may vary by subject and question.

Tagged in

Math

Trigonometry

Trigonometric Ratios

Related Trigonometry Q&A

Find answers to questions asked by student like you

Show more Q&A

Q: Part (a) and part (b)

A: Given values of the trigonometric ratios are

Q: Did exact value using half-angle identities a) sin 22.5° b) cos75°

A: to evaluate the (exact , using radicals, etc) values of the given trigonometric ratios using standar...

Q: Cos theta=0.10452846Instructions are on the image*Find the 2 angles in the interval [0 degrees, 360 ...

A: First we take inverse cosine on both sides and find the value of theta .

Q: Use fundamental identities to simplify the expression cosx-cosx sin^2 x

A: We have to simplify the expression.Expression is given below:

Q: My questions are being asked in the pics below

A: As per norms , the first three questions are answered. To apply standard half angle formulae and de...

Q: Find csc B when a=3 and b=7. Suppose ABC is a right triangle with side lenghts a, b and c and right ...

A: given information

Q: Can someone explain me how to solve this equation?

A: Let us simplify the expression given.

Q: find the approximate values for all solutions to tan^2t -tan t -6 =0

A: Obtain the approximate values as follows.

Q: Sin theta= 0.52991926Instructions are on the image*Find the 2 angles in the interval [0 degrees, 360...

A: First we take sine inverse on both sides and with the use of calculator, we find the value of theta.

Image Transcriptionclose