5.30. Let G be a finite abelian group. Suppose that, for every n e N, there are at most n elements a e G satisfying a" = e. Show that G is cyclic.
5.30. Let G be a finite abelian group. Suppose that, for every n e N, there are at most n elements a e G satisfying a" = e. Show that G is cyclic.
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter3: Groups
Section3.3: Subgroups
Problem 16E: Prove that each of the following subsets H of GL(2,C) is subgroup of the group GL(2,C), the general...
Related questions
Question
100%
Could you explain how to show 5.30 in detail? I also included lists of definitions and theorems in the book as a reference.
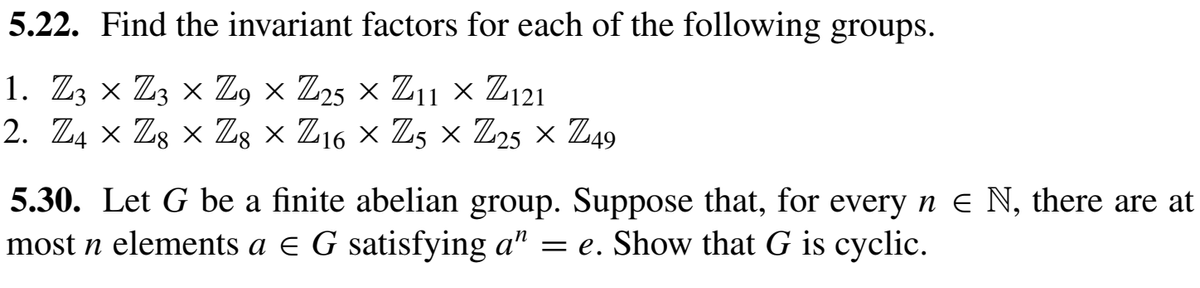
Transcribed Image Text:5.22. Find the invariant factors for each of the following groups.
1. Z3 × Z3 × Z, × Z25 × Z11 × Z121
2. Z4 × Zg × Z; × Z16 × Z5 × Z25 × Z49
5.30. Let G be a finite abelian group. Suppose that, for every n e N, there are at
most n elements a e G satisfying a" = e. Show that G is cyclic.

Transcribed Image Text:Definition 5.4. Let G be a nontrivial finite abelian
group,
and
say
that G
H2 x ... x Hk, where each H; is cyclic of order p", for some prime p; and positive
integer n;. Then the elementary divisors of G are the numbers p"', p"², .. , p*
where the order in this list is irrelevant, but each number must be listed as many
times as it occurs. The trivial group has no elementary divisors.
Definition 5.5. Let G be an abelian group and n a positive integer. Then we write
G" = {a" : a e G}.
Lemma 5.7. Let G and H be abelian groups and n a positive integer. Then
1. G" is a subgroup of G; and.
2. if a : G → H is an onto homomorphism, then a(G")
= H".
Theorem 5.6. Let G and H be finite abelian groups. Then G and H are isomorphic
if and only if they have the same elementary divisors.
Theorem 5.7 (Invariant Factor Decomposition). Suppose that G is a nontrivial
finite abelian group. Then G = Hị × H2 x ..x Hk, where each H; is a cyclic
subgroup of G of order m;, with m1 > 1 and m;|m;+1, for 1<i < k.
Definition 5.6. If G is isomorphic to Zm, ×
for 1 < i < k, then the numbers m1, ... ,
x ….× Zm, where m1 > 1 and m¡|m¡+1,
mk are called the invariant factors of G.
Theorem 5.8. Let G and H be nontrivial finite abelian groups. Then G and H are
isomorphic if and only if they have the same invariant factors.
Example 5.10. The elementary divisors of Z, × Z9 × Z3 × Z125 are 9, 9, 3, 125.
Example 5.11. To find the elementary divisors of Z300 × Z3, we use Theorem 5.4 to
see that the group is isomorphic to Z25 × Z4 × Z3 × Z3, so the elementary divisors
are 4, 3, 3, 25.
Example 5.12. The five abelian groups of order 16 listed in Example 5.7 are all non-
isomorphic, as they have different elementary divisors. Similarly for the six abelian
groups of order 200 given in Example 5.9.
Example 5.13. Let G = Z200 × Zg × Z6, H = Z120 × Z10 × Z4 × Z2 and K =
Z25 x Z24 x Z; × Z2. These are all abelian groups of order 9600. However, using
Theorem 5.4, we see that G is isomorphic to Zg × Z25 × Zg × Z3 × Z2, so its
elementary divisors are 8, 8, 2, 3, 25. Similarly, H is isomorphic to Z3 × Zg × Z5 x
Z5 x Z2x Z4 xZ2, so its elementary divisors are 8, 4, 2, 2, 3, 5, 5 and K is isomorphic
to Z25 x Z3 × Zg × Zg × Z2, so its elementary divisors are 8, 8, 2, 3, 25. Therefore,
G and K are isomorphic, but H is not isomorphic to either of them.
6.
Example 5.14. Let us use our work in Example 5.9 to find the invariant factors of the
abelian groups of order 200. We apply the method from Theorem 5.7. Considering
Z4 x Z2 x Z25, we see that the highest power of 2 that appears is 4, and the highest
power of 5 is 25. Therefore, m = 4.25 = 100. Deleting Z4 and Z25, we are left with
Z2, so mk-1 = 2, and we are finished. Thus, our group is isomorphic to Z2 × Z100,
so the invariant factors are 2, 100. When we examine Z2 x Z2 x Z2 × Z5 x Zs, we
see that mk =
2·5 = 10. Deleting Z2 and Z5, we are left with Z2 x Z2 x Z5. Thus,
mk-1 = 2 ·5 = 10. Deleting Z2 and Z5, we are left only with Z2. Thus, mk-2 = 2,
and we are finished. Therefore, our group is isomorphic to Z2 × Z10 × Z10, which
gives invariant factors of 2, 10, 10. Considering Zg × Z25, we simply get Z200, so 200
is the only invariant factor. Looking at Z2 × Z2 × Z2 × Z25, we have Z2 × Z2 × Z50,
so the invariant factors are 2, 2, 50. When we examine Zg x Z5 x Z5, we obtain
Z5 x Z40, so the invariant factors are 5, 40. Finally, if we take Z4 x Z2 x Z5 x Z5,
then we get Z10 × Z20, so the invariant factors are 10, 20.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,