9.6. Let R be a commutative ring. If I = {a e R : a" = 0 for some n e N}, show that I is an ideal of R.
9.6. Let R be a commutative ring. If I = {a e R : a" = 0 for some n e N}, show that I is an ideal of R.
Elements Of Modern Algebra
8th Edition
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Gilbert, Linda, Jimmie
Chapter6: More On Rings
Section6.4: Maximal Ideals (optional)
Problem 5E
Related questions
Topic Video
Question
100%
Could you explain how to show 9.6 in detail? I included list of theorems and definitions from the textbook.
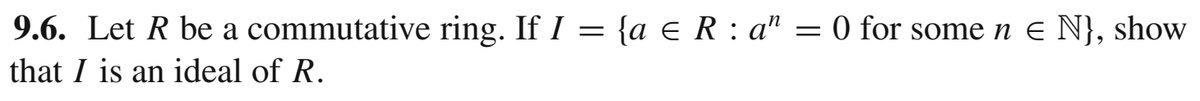
Transcribed Image Text:9.6. Let R be a commutative ring. If I = {a e R : a" = 0 for some n e N}, show
%3D
that I is an ideal of R.
![Definition 9.1. Let R be a ring. Then a subring I of R is said to be an ideal if
ir, ri e I for all i e I and r e R. We call this the absorption property.
Theorem 9.1. Let R be a ring and I a subset of R. Then I is an ideal if and only if
1. 0 e I;
2. i – je I for all i, j e I; and
3. ir, ri e I for all i e I, r e R.
Example 9.1. Let n be any integer. Then nZ is an ideal of Z. Indeed, we already know
that it is a subring. But also, if nk e nZ, then for any integerr,r(nk) = n(rk) E nZ.
Example 9.2. Let I be the set of all polynomials f (x) e R[x] such that f (0) = 0.
We claim that I is an ideal in R[x]. Certainly I contains the zero polynomial. Also, if
f (0) = g(0) = 0, then (f – )(0) = ƒ (0) – g(0) = 0, hence f (x)–g(x) e I.Also,
if f(0) = 0 and h(x) e R[x], then h(0) f (0) = h(0)0 = 0. Hence, h(x)f (x) e I.
|
Example 9.3. Let I be the set of all polynomials in Z[x] whose constant term is a
multiple of 5. Then I is an ideal. See Exercise 9.2.
Example 9.4. For any ring R, {0} and R are ideals of R.
Example 9.5. In Q, the ring of integers is a subring but not an ideal. Indeed, 3 e Z,
but 3(1/5) ¢ Z. Thus, Z does not have the absorption property.
Theorem 9.2. Let R be a ring with identity. If an ideal I of R contains a unit, then
I = R.
Corollary 9.1. Let F be a field. Then the only ideals of F are {0} and F.
Example 9.6. In Z, if we let I = 4Z and J = 6Z, then I + J = 2Z. Indeed, if
m e I +J, then m = 4a+6b = 2(2a+3b), for some integers a and b. In particular,
I+JC 2Z. On the other hand, for any c e Z, 2c = 4(-c)+6c e I + J, and hence
2Z CI+ J. We can say something more general here. See Exercise 9.4.
Theorem 9.3. If I and J are ideals of a ring R, then so is I + J.
Theorem 9.4. Let I and J be ideals in a ring R. Then I J is also an ideal.
Definition 9.2. Let R be a commutative ring with identity and a e R. Then the
principal ideal generated by a, denoted (a), is the set {ra :r e R}.
Example 9.7. In Z, we have (n) = nZ for any n e Z.
Example 9.8. The ideal from Example 9.2 is (x). Indeed, if f(x) € R[x], then
f (0) = 0 if and only if the constant term is 0; that is, if and only if the polynomial
is a multiple of x.
Theorem 9.5. If R is a commutative ring with identity, and a e R, then (a) is an
ideal of R; indeed, it is the intersection of all ideals of R containing a.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fe15ed467-90ec-4e60-afef-3d3f6119f74d%2F68e03d93-00c9-43c9-a42b-946f95c2ef52%2F1pfu92d_processed.png&w=3840&q=75)
Transcribed Image Text:Definition 9.1. Let R be a ring. Then a subring I of R is said to be an ideal if
ir, ri e I for all i e I and r e R. We call this the absorption property.
Theorem 9.1. Let R be a ring and I a subset of R. Then I is an ideal if and only if
1. 0 e I;
2. i – je I for all i, j e I; and
3. ir, ri e I for all i e I, r e R.
Example 9.1. Let n be any integer. Then nZ is an ideal of Z. Indeed, we already know
that it is a subring. But also, if nk e nZ, then for any integerr,r(nk) = n(rk) E nZ.
Example 9.2. Let I be the set of all polynomials f (x) e R[x] such that f (0) = 0.
We claim that I is an ideal in R[x]. Certainly I contains the zero polynomial. Also, if
f (0) = g(0) = 0, then (f – )(0) = ƒ (0) – g(0) = 0, hence f (x)–g(x) e I.Also,
if f(0) = 0 and h(x) e R[x], then h(0) f (0) = h(0)0 = 0. Hence, h(x)f (x) e I.
|
Example 9.3. Let I be the set of all polynomials in Z[x] whose constant term is a
multiple of 5. Then I is an ideal. See Exercise 9.2.
Example 9.4. For any ring R, {0} and R are ideals of R.
Example 9.5. In Q, the ring of integers is a subring but not an ideal. Indeed, 3 e Z,
but 3(1/5) ¢ Z. Thus, Z does not have the absorption property.
Theorem 9.2. Let R be a ring with identity. If an ideal I of R contains a unit, then
I = R.
Corollary 9.1. Let F be a field. Then the only ideals of F are {0} and F.
Example 9.6. In Z, if we let I = 4Z and J = 6Z, then I + J = 2Z. Indeed, if
m e I +J, then m = 4a+6b = 2(2a+3b), for some integers a and b. In particular,
I+JC 2Z. On the other hand, for any c e Z, 2c = 4(-c)+6c e I + J, and hence
2Z CI+ J. We can say something more general here. See Exercise 9.4.
Theorem 9.3. If I and J are ideals of a ring R, then so is I + J.
Theorem 9.4. Let I and J be ideals in a ring R. Then I J is also an ideal.
Definition 9.2. Let R be a commutative ring with identity and a e R. Then the
principal ideal generated by a, denoted (a), is the set {ra :r e R}.
Example 9.7. In Z, we have (n) = nZ for any n e Z.
Example 9.8. The ideal from Example 9.2 is (x). Indeed, if f(x) € R[x], then
f (0) = 0 if and only if the constant term is 0; that is, if and only if the polynomial
is a multiple of x.
Theorem 9.5. If R is a commutative ring with identity, and a e R, then (a) is an
ideal of R; indeed, it is the intersection of all ideals of R containing a.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,