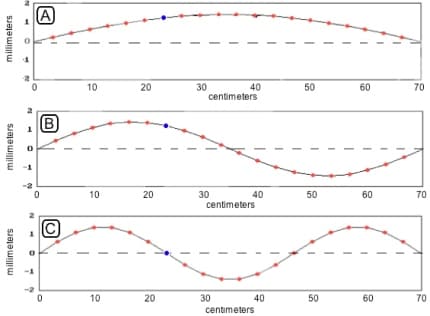
In the figure at the right is shown three graphs of the shapes of the same taut elastic string in three different circumstances, labeled A, B, and C. In some of the problems below, the string represents a guitar string, tied down at both ends, while in others, it is part of a very long telephone wire whose ends are not shown. Be careful to note which is which for each problem! The string is light enough that the effects of gravity can be ignored. In each case, the bit of string at the position x = 23 cm is painted blue.
1. Suppose the three graphs all represent the same string, tied down at x = 0 and x = 70 cm, and at the same tension. What can you say about the three frequencies of oscillation?
2. Suppose the three graphs all represent the same string, tied down at x = 0 and x = 70 cm, but their tensions have been adjusted so that all three situations are all oscillating at the same frequency. What can you say about the tensions in the three cases?
3. Suppose that graph C represents the string, tied down at x = 0 and x = 70 cm, under tension. What can you say about the acceleration of the blue bead in case C at the instant shown?
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images






