Elementary Geometry For College Students, 7e
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
Bartleby Related Questions Icon

Related questions

Q: For the AAS Theorem to apply, which side of the triangle must be known? A. the included side A. the…
A: For AAS theorem two angles and a non-included side is congruent then both triangles are congruent.
Q: ABC is a triangle and AD is any line drawn from A to the base BC. From B and C, two perpendiculars…
A: Given- ABC is a triangle and AD is any line drawn from A to the base BC. From B and C, two…
Q: Which of these statements is true for all trapezoids? OA. one pair of sides are parallel B. base…
A: Firstly lets have look upon trapezoids  Properties of Trapezoid These are the properties of a…
Q: A D F Using only the marking in the diagram, what theorem can be used to show that the two triangles…
A: Solution: Two triangles are said to be congruent if the three sides and the three…
Q: 13) In the diagram below, BC connects points B and C on the congruent sides of isosceles triangle…
A: We have to find the length of BC from the given figure.
Q: Determine whether the triangles are congruent. Complete the explanation of your reasonin A C 1.5 m…
A: Prove congruence of triangle
Q: 60. If AC = 18, BE = 13, DE = 3 and D is the midpoint of CE, what is AB? %3D %3D А В A C E A. 10 В.…
A: Given: AC=18, BE=13, DE=3 and D is mid point of CE Now, if D is midpoint of CE then CE=2DE=23=6
Q: In quadrilateral ABCD, the diagonals intersect at point T. Thomas has used the Alternate Interior…
A: Concept: Congruency: Triangle congruence: Two triangles are said to be congruent if their three…
Q: Select the correct answer. With which information can you construct a unique rhombus? O A.…
A:
Q: 18. Which statement does not demonstrate the corollary to the triangle exterior angle theorem? y/c…
A: We will take help of given theorem.
Q: Given: BE = BD and ZABE = ZCBD. Prove: AABC is an isosceles triangle. Reason Given Select a…
A: Given, BE¯ ≅ BD¯  and  ∠ABE ≅ ∠CBD  We have to prove ∆ABC is an isosceles triangle.
Q: ABC is a right angled triangle right angled at B. If P and Q are the mid - points of the sides AB…
A: Given:
Q: Consider the following pentagon. Which of the following is false? V OA. = v - w OB. AD = u + v +r…
A:
Q: Given: BD is the angle bisector of ZABC and ZADC. | Prove: ΔΑBDΔCBD A B Statements D Reasons 1) ? 1)…
A:
Q: What is the best answer for Reason 2? * Complete the proof below. Given: ZBAC = LDAC, B AC 1 BD A-…
A:
Q: Which statement is true about the angle bisectors of a triangle? O A. They bisect the sides of the…
A: Angle bisectors intersect at a point which is called incenter. The incenter is equidistant from all…
Q: Given, A DEF is an isoceles triangle with LD Ver ted angle. as the ,. DE DF E F DE = 4x-7 EF 3x +2…
A: Given that DE=DF So, 4x-7=6x-1515-7=6x-4x8=2xx=82x=4
Q: Which statement is true about the angle bisector AD of AABC? O A. AD is a perpendicular bisector of…
A: We can make it easier for you
Q: hich of the following statements is true? B A E O A. point E is the midpoint of segment AT B. the…
A: Answer :- Point E is the midpoint of segment AC.
Q: In the triangle ABC let D be the midpoint of BC then prove that AB2 + AC? 2(AD² + BD²)?
A:
Q: Based on the image below, which theorem/postulate would prove triangle a RST and RUT congruent by…
A: Here , RT is perpendicular bisector of SU .
Q: 2. Circe the theorem, if any, that can be used to prove the two triangles are congruent. A E F D a.…
A:
Q: In ? ABC, AD is the perpendicular bisector of BC. Show that ? ABC is an isosceles triangle in which…
A: Consider the following figure: AD is the perpendicular bisector of BC. BD=CD In △ABD, use…
Q: Which of the following theorems could be used to prove the two triangle are congruent? D E %3 C O…
A: Two shapes that are of the same size and the same shape are congruent Two triangles are said to…
Q: Given: C is the midpoint of BD and AE Piove ΔΑBC = ΔΕDC D STATEMENTS REASONS 1. Cis a midpoint of BD…
A: In the given ΔABC and ∆EDC C is the mid point of BD and AE
Q: 8. Glven: Parallelogram ABCD Is shown wiih BD drawn as shown, Prove: AB = CD, BC a DA C. A…
A: We show here two triangle congruent by ASA theorem.
Q: 1. Based on the information presented on the picture, determine all the true statements. ZAEB is an…
A:
Q: 8. Find the value of z using the Triangle Angle Bisector Theorem. A 16 12 B 8 O 12 16
A:
Q: m In the diagram, line / is parallel to line m. How would you prove A QUA A ADQ? 'A .... ....…
A:
Q: Prove the following result, needed to demonstrate the Saccheri- Legendre theorem (see Figure 4.27).…
A: Given, D is the midpoint of BC And E is the unique point on AD Such that, AD=DE Angle sum of △AEC…
Q: 7. Which of the following conditions would make triangle ADB similar to triangle ABC? B D A.O AD ВС…
A: For the given statement
Q: Suppose CM and DM intersect at AB as shown. M Alison states that ZAMC + ZCMD+ ZDMB= ZAMB. Which…
A:
Q: Sam is studying a geometric drawing. He observes that zPQR and LAQB are obtuse vertical angles and…
A:
Q: (True or false) For a given triangle ABC with AC > AB. If D is a point on BC such that AD is…
A: “Since you have asked multiple questions, we will solve the first question for you. If you want any…
Q: D is the midpoint of AC, ED congruent to FD, angle EDA congruent to angle FDC. Prove AB congruent to…
A: Topic:- geometry
Q: Jim is given two triangles, PQR and EFG, with PQ = EF, PR = FG, and  angle QPR > angle FEG. Jim…
A:
Q: 34. Which rule explains why these triangles are congruent? A ASA B SAS AAS D SSs
A:
Q: Label a point D outside AABC so that AD WY and ZDAB ZYWX. Since WX AB, AWXY AABD by Now, let E be…
A:
Q: Fill in the reasons to complete the following proof. Given: AB || DC, AB DOC Prove: M is the…
A:
Q: A triangle is drawn (Refer to figure 2). ET is perpendicular bisector of HP. State why EH = EP. A.…
A: Perpendicular bisector:- A-line segment perpendicular to and passing through the midpoint.
Q: 29. In triangle GHJ below, points A, B and C are midpoints of the sides. А G When AB 3x + 8 and GJ =…
A:
Q: are the mid-points of BC and AC In Figure 2, ABC is a triangle. M and N respectively. D is a point…
A:
Q: Line AE is parallel to FD ae is congruent to FD and AC is congruent to BD prove triangle aec is…
A:
Q: 2 In the triangle ABC, the point D divides the line AB in the ratio 1:3 and E divides the line AC…
A: Given that in the triangle ABC , the point D divides the line AB in the ratio 1:3 and E divides the…
Q: Decide whether enough information is given to prove the two triangles are congruent. If there is…
A:
Q: B. Determine if enough information is given to show that the triangles congruent. If so, write the…
A:
Q: II. Prove: The bisector of an angle intersect any segment which joins the sides of the angles .…
A:
bartleby

Concept explainers

Statements and Logic
Logic is the analysis of general patterns of thoughts without regard to any specific sense of context.
Question

Please help fill in the blanks of the two-column proof.

The proof is in the picture.

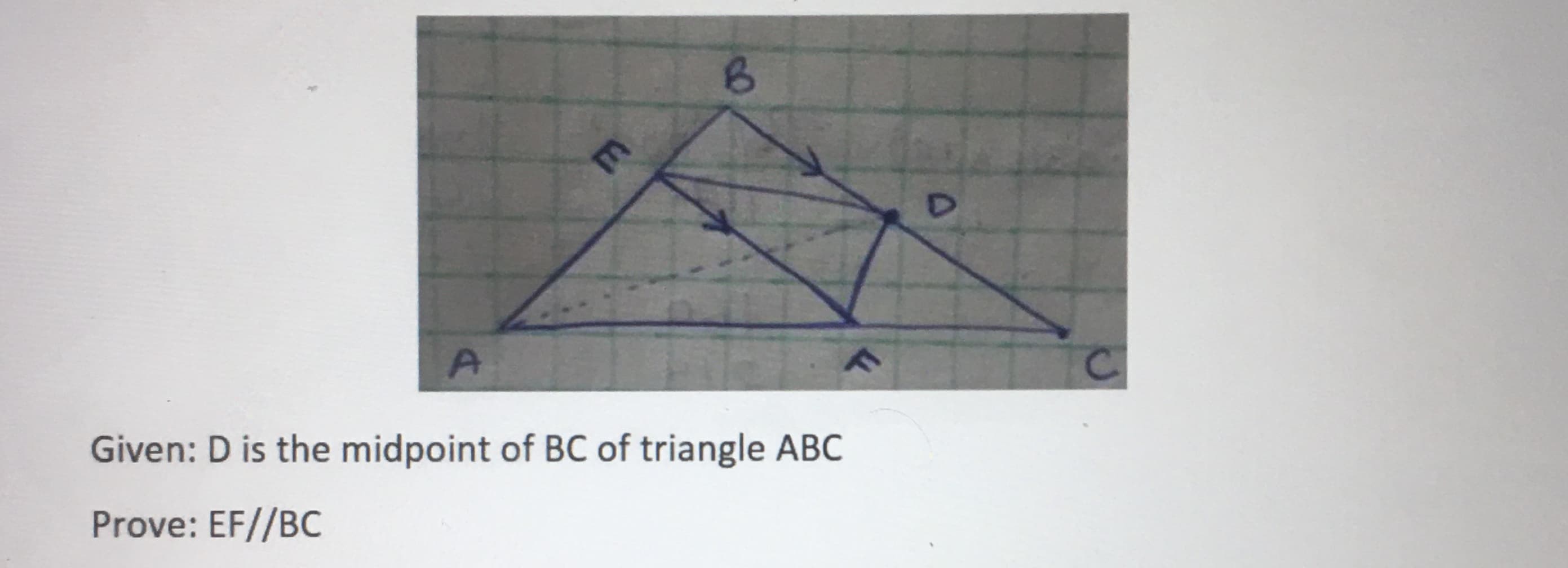
A. C. Given: D is the midpoint of BC of triangle ABC Prove: EF//BC E.
expand button
Transcribed Image Text:A. C. Given: D is the midpoint of BC of triangle ABC Prove: EF//BC E.
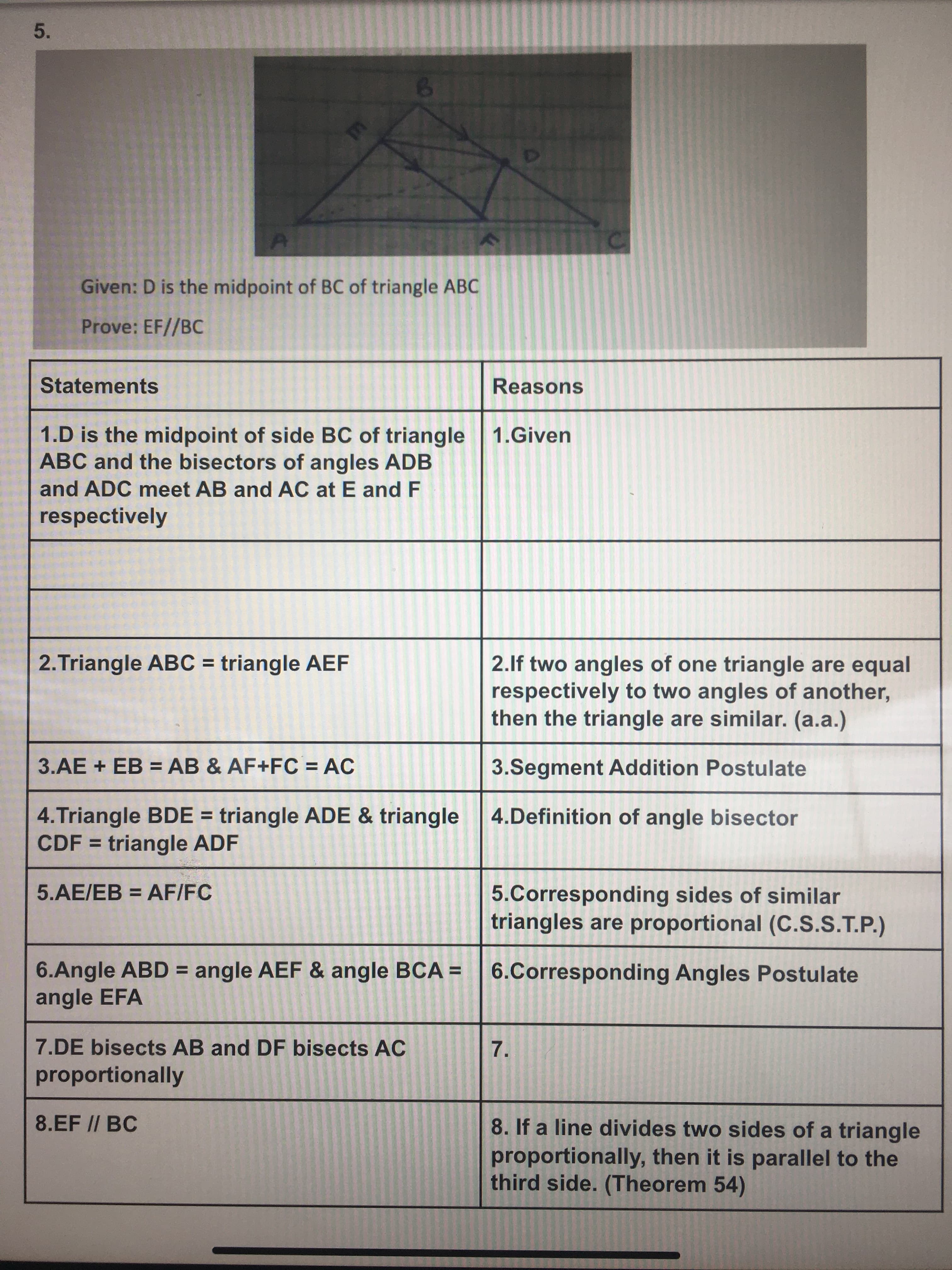
6. Given: D is the midpoint of BC of triangle ABC Prove: EF//BC Statements Reasons 1.D is the midpoint of side BC of triangle 1.Given ABC and the bisectors of angles ADB and ADC meet AB and AC at E and F respectively 2.Triangle ABC = triangle AEF 2.lf two angles of one triangle are equal respectively to two angles of another, then the triangle are similar. (a.a.) 3.AE + EB = AB & AF+FC = AC 3.Segment Addition Postulate 4.Triangle BDE = triangle ADE & triangle CDF = triangle ADF 4.Definition of angle bisector 5.AE/EB = AF/FC 5.Corresponding sides of similar triangles are proportional (C.S.S.T.P.) 6.Angle ABD = angle AEF & angle BCA = angle EFA 6.Corresponding Angles Postulate 7.DE bisects AB and DF bisects AC proportionally 8.EF II BC 8. If a line divides two sides of a triangle proportionally, then it is parallel to the third side. (Theorem 54) 7. 5.
expand button
Transcribed Image Text:6. Given: D is the midpoint of BC of triangle ABC Prove: EF//BC Statements Reasons 1.D is the midpoint of side BC of triangle 1.Given ABC and the bisectors of angles ADB and ADC meet AB and AC at E and F respectively 2.Triangle ABC = triangle AEF 2.lf two angles of one triangle are equal respectively to two angles of another, then the triangle are similar. (a.a.) 3.AE + EB = AB & AF+FC = AC 3.Segment Addition Postulate 4.Triangle BDE = triangle ADE & triangle CDF = triangle ADF 4.Definition of angle bisector 5.AE/EB = AF/FC 5.Corresponding sides of similar triangles are proportional (C.S.S.T.P.) 6.Angle ABD = angle AEF & angle BCA = angle EFA 6.Corresponding Angles Postulate 7.DE bisects AB and DF bisects AC proportionally 8.EF II BC 8. If a line divides two sides of a triangle proportionally, then it is parallel to the third side. (Theorem 54) 7. 5.
Expert Solution
Check Mark
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Geometry
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.
Similar questions
  • In the drawing, suppose that ZX is the perpendicular bisector of WY. What type of quadrilateral is WXYZ?
    In the drawing, ABDCEF with transversals l and m. If D and C are the midpoints of AE and BF, respectively, then is trapezoid ABCD similar to trapezoid DCFE?
    In the drawing, suppose that WY and XZ bisect each other. What type of quadrilateral is WXYZ?
  • In ABC, M is the midpoint of AB and N is the midpoint of AC. If MN= 3x-11 and BC= 4x24, find the value of x._
    In O with diameter AC, OC=5 and AB=6. If M is the midpoint of BC, find AM.
    Suppose that square RSTV slides point for point to form quadrilateral WXYZ. a Is WXYZ a square ? b Is ? RSTVWXYZ c Is RS=1.8cm, find WX.
  • Consider regular pentagon RSTVQ not shown. Given that diagonals QT and VR intersect at point F, show that VFFR=TFFQ.
    A carpenter has placed a square over an angle in such a manner that ABAC and BDCD. In the drawing, what can you conclude about the location of point D?
    Use the Pythagorean Theorem to find the length of the hypotenuse in the triangle shown below.
  • For a given triangle such as ABC, what word describes the point of concurrency for athe three perpendicular bisectors of sides? bthe three altitudes?
    What type of trapezoid a has congruent diagonals. b has congruent base angles.
    For Exercises 39 to 44, make drawings as needed. Can two spheres a be internally tangent? b have no points in common?
    • SEE MORE QUESTIONS
    Recommended textbooks for you
  • Elementary Geometry For College Students, 7e
    Geometry
    ISBN:9781337614085
    Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
    Publisher:Cengage,
    Holt Mcdougal Larson Pre-algebra: Student Edition...
    Algebra
    ISBN:9780547587776
    Author:HOLT MCDOUGAL
    Publisher:HOLT MCDOUGAL
    Elementary Geometry for College Students
    Geometry
    ISBN:9781285195698
    Author:Daniel C. Alexander, Geralyn M. Koeberlein
    Publisher:Cengage Learning
  • Elementary Algebra
    Algebra
    ISBN:9780998625713
    Author:Lynn Marecek, MaryAnne Anthony-Smith
    Publisher:OpenStax - Rice University
    • Elementary Geometry For College Students, 7e
    Geometry
    ISBN:9781337614085
    Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
    Publisher:Cengage,
    Holt Mcdougal Larson Pre-algebra: Student Edition...
    Algebra
    ISBN:9780547587776
    Author:HOLT MCDOUGAL
    Publisher:HOLT MCDOUGAL
    Elementary Geometry for College Students
    Geometry
    ISBN:9781285195698
    Author:Daniel C. Alexander, Geralyn M. Koeberlein
    Publisher:Cengage Learning
    Elementary Algebra
    Algebra
    ISBN:9780998625713
    Author:Lynn Marecek, MaryAnne Anthony-Smith
    Publisher:OpenStax - Rice University
    SEE MORE TEXTBOOKS