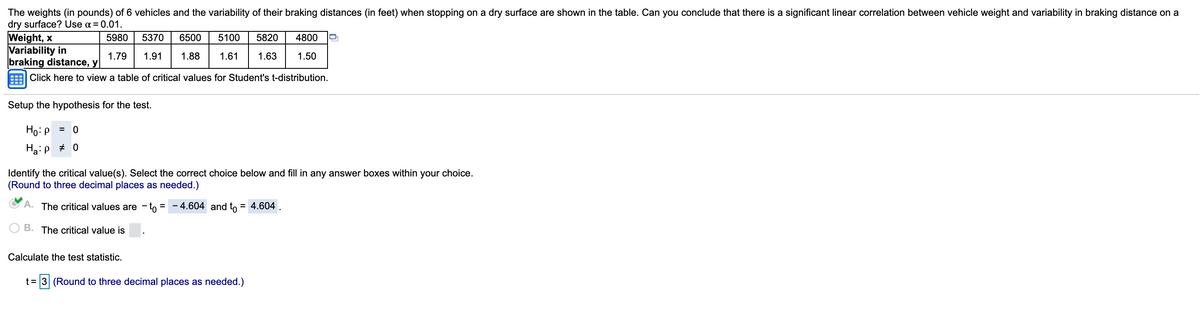
Help me answer last two The weights (in pounds) of 6 vehicles and the variability of their braking distances (in feet) when stopping on a dry surface are shown in the table. Can you conclude that there is a significant linear correlation between vehicle weight and variability in braking distance on adry surface? Use a = 0.01.Weight, xVariability inbraking distance, y5980537065005100582048001.791.911.881.611.631.50Click here to view a table of critical values for Student's t-distribution.Setup the hypothesis for the test.Ho:p = 0Ha:p + 0Identify the critical value(s). Select the correct choice below and fill in any answer boxes within your choice.(Round to three decimal places as needed.)A. The critical values are - to = - 4.604 and to = 4.604B. The critical value isCalculate the test statistic.t = 3 (Round to three decimal places as needed.) What is your conclusion?ThereV enough evidence at the 1% level of significance to conclude that therea significant linear correlation between vehicle weight and variability in braking distance on a dry surface.

Name: Help me answer last two The weights (in pounds) of 6 vehicles and the
Uploaded: 2024-03-20T07:07:37.000Z
Channel: Bartleby
Description: Help me answer last two The weights (in pounds) of 6 vehicles and the variability of their braking distances (in feet) when stopping on a dry surface are shown in the table. Can you conclude that there is a significant linear correlation between vehi