Chapter 10, Problem 023 Your answer is partially correct. Try again A flywheel with a diameter of 1.73 m is rotating at an angular speed of 268 rev/min. (a) What is the angular speed of the flywheel in radians per second? (b) What is the linear speed of a point on the rim of the flywheel? (c) What constant angular acceleration (in revolutions per minute-squared) will increase the wheel's angular speed to 1200 rev/min in 131 s? (d) How many revolutions does the wheel make during that 131 s? Units rad/s (a) Number 28.0 (b) NumberT24,2 Units m/s Unit rev/min 2 (c) Number 426 Units rev (d) NumberT [264
Chapter 10, Problem 023 Your answer is partially correct. Try again A flywheel with a diameter of 1.73 m is rotating at an angular speed of 268 rev/min. (a) What is the angular speed of the flywheel in radians per second? (b) What is the linear speed of a point on the rim of the flywheel? (c) What constant angular acceleration (in revolutions per minute-squared) will increase the wheel's angular speed to 1200 rev/min in 131 s? (d) How many revolutions does the wheel make during that 131 s? Units rad/s (a) Number 28.0 (b) NumberT24,2 Units m/s Unit rev/min 2 (c) Number 426 Units rev (d) NumberT [264
Principles of Physics: A Calculus-Based Text
5th Edition
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Raymond A. Serway, John W. Jewett
Chapter10: Rotational Motion
Section: Chapter Questions
Problem 11P: A disk 8.00 cm in radius rotates at a constant rate of 1200 rev/min about its central axis....
Related questions
Question
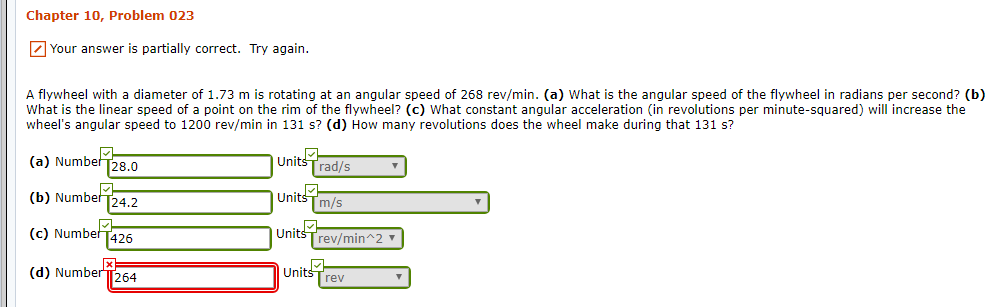
Transcribed Image Text:Chapter 10, Problem 023
Your answer is partially correct. Try again
A flywheel with a diameter of 1.73 m is rotating at an angular speed of 268 rev/min. (a) What is the angular speed of the flywheel in radians per second? (b)
What is the linear speed of a point on the rim of the flywheel? (c) What constant angular acceleration (in revolutions per minute-squared) will increase the
wheel's angular speed to 1200 rev/min in 131 s? (d) How many revolutions does the wheel make during that 131 s?
Units
rad/s
(a) Number 28.0
(b) NumberT24,2
Units
m/s
Unit
rev/min 2
(c) Number
426
Units rev
(d) NumberT
[264
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images

Recommended textbooks for you

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Physics for Scientists and Engineers: Foundations…
Physics
ISBN:
9781133939146
Author:
Katz, Debora M.
Publisher:
Cengage Learning

College Physics
Physics
ISBN:
9781938168000
Author:
Paul Peter Urone, Roger Hinrichs
Publisher:
OpenStax College

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Glencoe Physics: Principles and Problems, Student…
Physics
ISBN:
9780078807213
Author:
Paul W. Zitzewitz
Publisher:
Glencoe/McGraw-Hill