Conceptual Problem about Projectile Motion 4 of 4 Review | Constants Learning Goal: Part D To understand projectile motion by considering horizontal constant velocity motion and vertical constant acceleration motion independently If a second ball were dropped from rest from height yma how long would it take to reach the ground? Ignore air resistance. Projectile motion refers to the motion of unpowered objects (callled projectiles) such as balls or stones moving near the surface of the earth under the influence of the earth's gravity alone. In this analysis we assume that air resistance can be neglected. Check all that apply View Available Hint(s) An object undergoing projectile motion near the surface of the earth obeys the following rules: to 1. An object undergoing projectile motion travels horizontally at a constant rate. That is, the x component of its velocity, , is constant ti to 2. An object undergoing projectile motion moves vertically with a constant downward acceleration whose magnitude, denoted by g, is equal to 9.80 m/s2 near surface continuously 3. An object undergoing projectile motion will undergo the horizontal and vertical t the earth. Hence, the y component of its velocity, uy, changes of t2-t tto motions described above from the instant it is launched until the instant it strikes the ground again. Even though the horizontal and vertical motions can be treated independently, they are related by the fact that they occur for exactly the same amount of time, namely the time t the projectile is in the air Submit the ball refers to how far it moves horizontally, from just after it is launched until just before it lands. Range is defined as O, or just 2 in this particular situation since o= 0. The range Range can be calculated as the product of the flight time ta and the x component of the velocity vr (which is the same at all times, so vr = upz). The value of v, can be found from the launch speed up and the launch angle 0 using trigonometric functions, as was done in Part B. The flight time is related to the in itial y component of the velocity, which may also be found from th and e using trig functions. The following equations may be useful in solving projectile motion problems, but these equations apply only to a projectile launched over level ground from position (xo = = 0) at time to 0with initial speed u and launch angle emeasured from the horizontal. As was the case above, t refers to the flight time and R refers to the range of the projectile. 2u sin(0) Figure > 1 of 2 flight time: t = sin(20) range: R t,= t peak height Ут or ymax In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that achieves the maximum range for projectile motion over level ground is 45 degrees range X or R Part E Which of the following changes would increase the range of the ball shown in the original figure? 0 Distance Downrange Check all that apply. initial position (Хо- Уо) Increase u above 30 m/s Reduce u below 30 m/s. Height Conceptual Problem about Projectile Motion 4 of 4 Review | Constants Learning Goal: t-t To understand projectile motion by considering horizontal constant velocity motion and vertical tz to constant acceleration motion independently. Projectile motion refers to the motion of unpowered objects (called projectiles) such as balls or stones moving near the surface of the earth under the influence of the earth's gravity alone. In this analysis we assume that air resistance can be neglected Submit An object undergoing projectile motion near the surface of the earth obeys the following rules: 1. An object undergoing projectile motion travels horizontally at a constant rate. That is, the x component of its velocity, , is constant 2. An object undergoing projectile motion moves vertically with a constant downward acceleration whose magnitude, denoted by g, is equal to 9.80 m/s2 near the surface of the earth. Hence, the y component of its velocity, u changes continuously The range R of the ball refers to how far it moves horizontally, from just after it is launched until just before it lands. Range is defined as -0, or just x2 in this particular situation since ro= 0. Range can be calculated as the product of the flight time ta and the x component of the velocity vr (which is the same at all times, so vr = upz). The value of v, can be found from the launch speed up and the launch angle 0 using trigonometric functions, as was done in Part B. The flight time is related to the in itial y component of the velocity, which may also be found from th and using trig functions. The following equations may be useful in solving projectile motion problems, but these equations apply only to a projectile launched over level ground from position (o = Yo = 0) at time to = 0with initial speed u and launch angle 0measured from the horizontal. As was the case above, ta refers to the flight time and R refers to the range of the projectile 3. An object undergoing projectile motion will undergo the horizontal and vertical motions described above from the instant it is launched until the instant it strikes the 2uo sin(0) 2t0y flight time: t ground again. Even though the horizontal and vertical motions can be treated independently, they are related by the fact that they occur for exactly the same amount of time, namely the time t the projectile is in the air. sin(20) range: R vt In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that achieves the maximum range for projectile motion over level ground is 45 degrees Part E Which of the following changes would increase the range of the ball shown in the original figure? Check all that apply. Figure 1 of 2 Increase uh above 30 m/s. peak height Reduce u below 30 m/s. у or ymax Reduce 0 from 60 degrees to 45 degrees. range Reduce 0 from 60 degrees to less than 30 degrees X2 or R Increase 0 from 60 degrees up toward 90 degrees. Лo ON Distance Downrange Submit Request Answer initial position (x- Yo
Conceptual Problem about Projectile Motion 4 of 4 Review | Constants Learning Goal: Part D To understand projectile motion by considering horizontal constant velocity motion and vertical constant acceleration motion independently If a second ball were dropped from rest from height yma how long would it take to reach the ground? Ignore air resistance. Projectile motion refers to the motion of unpowered objects (callled projectiles) such as balls or stones moving near the surface of the earth under the influence of the earth's gravity alone. In this analysis we assume that air resistance can be neglected. Check all that apply View Available Hint(s) An object undergoing projectile motion near the surface of the earth obeys the following rules: to 1. An object undergoing projectile motion travels horizontally at a constant rate. That is, the x component of its velocity, , is constant ti to 2. An object undergoing projectile motion moves vertically with a constant downward acceleration whose magnitude, denoted by g, is equal to 9.80 m/s2 near surface continuously 3. An object undergoing projectile motion will undergo the horizontal and vertical t the earth. Hence, the y component of its velocity, uy, changes of t2-t tto motions described above from the instant it is launched until the instant it strikes the ground again. Even though the horizontal and vertical motions can be treated independently, they are related by the fact that they occur for exactly the same amount of time, namely the time t the projectile is in the air Submit the ball refers to how far it moves horizontally, from just after it is launched until just before it lands. Range is defined as O, or just 2 in this particular situation since o= 0. The range Range can be calculated as the product of the flight time ta and the x component of the velocity vr (which is the same at all times, so vr = upz). The value of v, can be found from the launch speed up and the launch angle 0 using trigonometric functions, as was done in Part B. The flight time is related to the in itial y component of the velocity, which may also be found from th and e using trig functions. The following equations may be useful in solving projectile motion problems, but these equations apply only to a projectile launched over level ground from position (xo = = 0) at time to 0with initial speed u and launch angle emeasured from the horizontal. As was the case above, t refers to the flight time and R refers to the range of the projectile. 2u sin(0) Figure > 1 of 2 flight time: t = sin(20) range: R t,= t peak height Ут or ymax In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that achieves the maximum range for projectile motion over level ground is 45 degrees range X or R Part E Which of the following changes would increase the range of the ball shown in the original figure? 0 Distance Downrange Check all that apply. initial position (Хо- Уо) Increase u above 30 m/s Reduce u below 30 m/s. Height Conceptual Problem about Projectile Motion 4 of 4 Review | Constants Learning Goal: t-t To understand projectile motion by considering horizontal constant velocity motion and vertical tz to constant acceleration motion independently. Projectile motion refers to the motion of unpowered objects (called projectiles) such as balls or stones moving near the surface of the earth under the influence of the earth's gravity alone. In this analysis we assume that air resistance can be neglected Submit An object undergoing projectile motion near the surface of the earth obeys the following rules: 1. An object undergoing projectile motion travels horizontally at a constant rate. That is, the x component of its velocity, , is constant 2. An object undergoing projectile motion moves vertically with a constant downward acceleration whose magnitude, denoted by g, is equal to 9.80 m/s2 near the surface of the earth. Hence, the y component of its velocity, u changes continuously The range R of the ball refers to how far it moves horizontally, from just after it is launched until just before it lands. Range is defined as -0, or just x2 in this particular situation since ro= 0. Range can be calculated as the product of the flight time ta and the x component of the velocity vr (which is the same at all times, so vr = upz). The value of v, can be found from the launch speed up and the launch angle 0 using trigonometric functions, as was done in Part B. The flight time is related to the in itial y component of the velocity, which may also be found from th and using trig functions. The following equations may be useful in solving projectile motion problems, but these equations apply only to a projectile launched over level ground from position (o = Yo = 0) at time to = 0with initial speed u and launch angle 0measured from the horizontal. As was the case above, ta refers to the flight time and R refers to the range of the projectile 3. An object undergoing projectile motion will undergo the horizontal and vertical motions described above from the instant it is launched until the instant it strikes the 2uo sin(0) 2t0y flight time: t ground again. Even though the horizontal and vertical motions can be treated independently, they are related by the fact that they occur for exactly the same amount of time, namely the time t the projectile is in the air. sin(20) range: R vt In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that achieves the maximum range for projectile motion over level ground is 45 degrees Part E Which of the following changes would increase the range of the ball shown in the original figure? Check all that apply. Figure 1 of 2 Increase uh above 30 m/s. peak height Reduce u below 30 m/s. у or ymax Reduce 0 from 60 degrees to 45 degrees. range Reduce 0 from 60 degrees to less than 30 degrees X2 or R Increase 0 from 60 degrees up toward 90 degrees. Лo ON Distance Downrange Submit Request Answer initial position (x- Yo
University Physics Volume 1
18th Edition
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:William Moebs, Samuel J. Ling, Jeff Sanny
Chapter4: Motion In Two And Three Dimensions
Section: Chapter Questions
Problem 32P: A Lockheed Martin F-35 II lighting jet takes off from an aircraft carrier with a runway length of 90...
Related questions
Question
How do you solve these? Can you show steps?
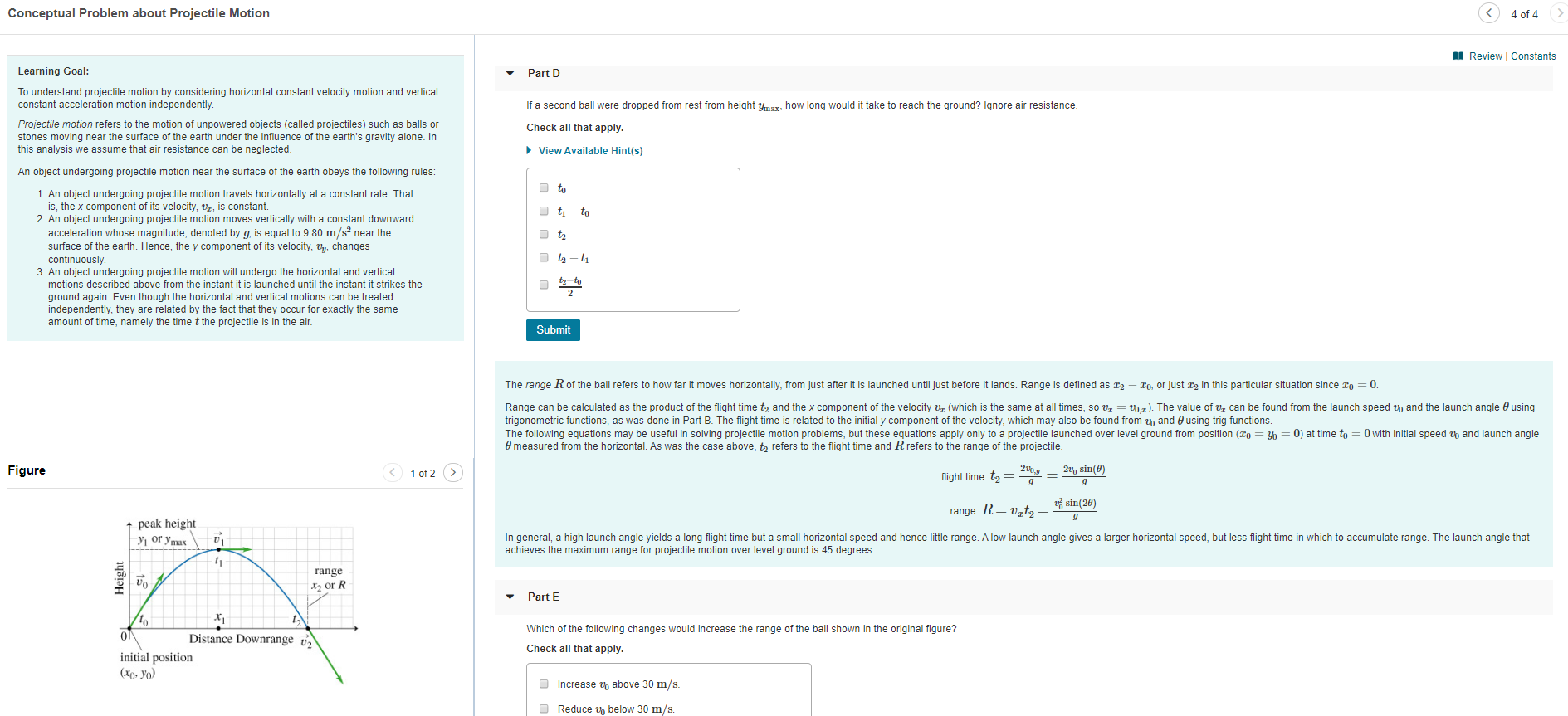
Transcribed Image Text:Conceptual Problem about Projectile Motion
4 of 4
Review | Constants
Learning Goal:
Part D
To understand projectile motion by considering horizontal constant velocity motion and vertical
constant acceleration motion independently
If a second ball were dropped from rest from height yma how long would it take to reach the ground? Ignore air resistance.
Projectile motion refers to the motion of unpowered objects (callled projectiles) such as balls or
stones moving near the surface of the earth under the influence of the earth's gravity alone. In
this analysis we assume that air resistance can be neglected.
Check all that apply
View Available Hint(s)
An object undergoing projectile motion near the surface of the earth obeys the following rules:
to
1. An object undergoing projectile motion travels horizontally at a constant rate. That
is, the x component of its velocity, , is constant
ti
to
2. An object undergoing projectile motion moves vertically with a constant downward
acceleration whose magnitude, denoted by g, is equal to 9.80 m/s2 near
surface
continuously
3. An object undergoing projectile motion will undergo the horizontal and vertical
t
the earth. Hence, the y component of its velocity, uy, changes
of
t2-t
tto
motions described above from the instant it is launched until the instant it strikes the
ground again. Even though the horizontal and vertical motions can be treated
independently, they are related by the fact that they occur for exactly the same
amount of time, namely the time t the projectile is in the air
Submit
the ball refers to how far it moves horizontally, from just after it is launched until just before it lands. Range is defined as
O, or just 2 in this particular situation since o= 0.
The range
Range can be calculated as the product of the flight time ta and the x component of the velocity vr (which is the same at all times, so vr = upz). The value of v, can be found from the launch speed up and the launch angle 0 using
trigonometric functions, as was done in Part B. The flight time is related to the in itial y component of the velocity, which may also be found from th and e using trig functions.
The following equations may be useful in solving projectile motion problems, but these equations apply only to a projectile launched over level ground from position (xo = = 0) at time to 0with initial speed u and launch angle
emeasured from the horizontal. As was the case above, t refers to the flight time and R refers to the range of the projectile.
2u sin(0)
Figure
>
1 of 2
flight time: t
=
sin(20)
range: R t,=
t peak height
Ут or ymax
In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that
achieves the maximum range for projectile motion over level ground is 45 degrees
range
X or R
Part E
Which of the following changes would increase the range of the ball shown in the original figure?
0
Distance Downrange
Check all that apply.
initial position
(Хо- Уо)
Increase u above 30 m/s
Reduce u below 30 m/s.
Height
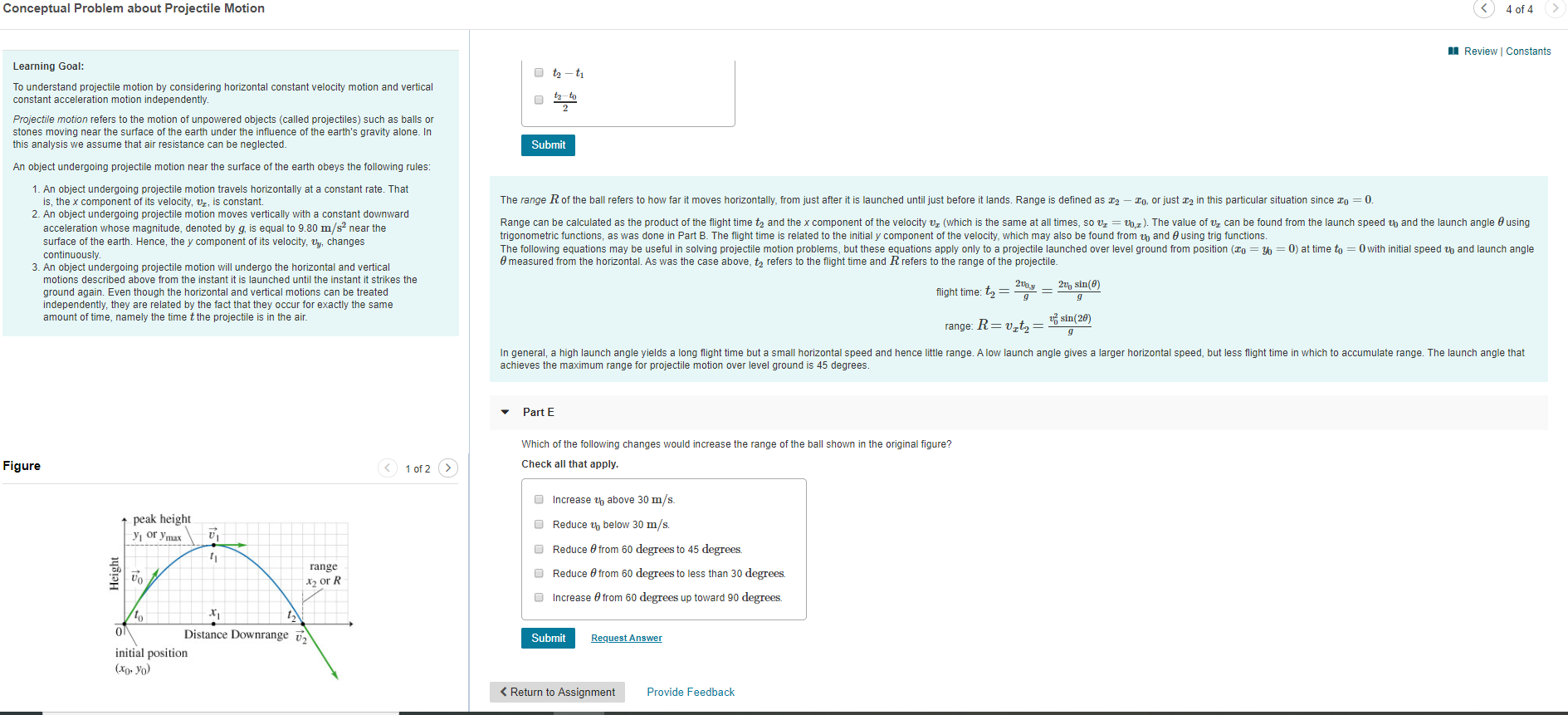
Transcribed Image Text:Conceptual Problem about Projectile Motion
4 of 4
Review | Constants
Learning Goal:
t-t
To understand projectile motion by considering horizontal constant velocity motion and vertical
tz to
constant acceleration motion independently.
Projectile motion refers to the motion of unpowered objects (called projectiles) such as balls or
stones moving near the surface of the earth under the influence of the earth's gravity alone. In
this analysis we assume that air resistance can be neglected
Submit
An object undergoing projectile motion near the surface of the earth obeys the following rules:
1. An object undergoing projectile motion travels horizontally at a constant rate. That
is, the x component of its velocity, , is constant
2. An object undergoing projectile motion moves vertically with a constant downward
acceleration whose magnitude, denoted by g, is equal to 9.80 m/s2 near the
surface of the earth. Hence, the y component of its velocity, u changes
continuously
The range R of the ball refers to how far it moves horizontally, from just after it is launched until just before it lands. Range is defined as -0, or just x2 in this particular situation since ro= 0.
Range can be calculated as the product of the flight time ta and the x component of the velocity vr (which is the same at all times, so vr = upz). The value of v, can be found from the launch speed up and the launch angle 0 using
trigonometric functions, as was done in Part B. The flight time is related to the in itial y component of the velocity, which may also be found from th and using trig functions.
The following equations may be useful in solving projectile motion problems, but these equations apply only to a projectile launched over level ground from position (o = Yo = 0) at time to = 0with initial speed u and launch angle
0measured from the horizontal. As was the case above, ta refers to the flight time and R refers to the range of the projectile
3. An object undergoing projectile motion will undergo the horizontal and vertical
motions described above from the instant it is launched until the instant it strikes the
2uo sin(0)
2t0y
flight time: t
ground again. Even though the horizontal and vertical motions can be treated
independently, they are related by the fact that they occur for exactly the same
amount of time, namely the time t the projectile is in the air.
sin(20)
range: R vt
In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that
achieves the maximum range for projectile motion over level ground is 45 degrees
Part E
Which of the following changes would increase the range of the ball shown in the original figure?
Check all that apply.
Figure
1 of 2
Increase uh above 30 m/s.
peak height
Reduce u below 30 m/s.
у or ymax
Reduce 0 from 60 degrees to 45 degrees.
range
Reduce 0 from 60 degrees to less than 30 degrees
X2 or R
Increase 0 from 60 degrees up toward 90 degrees.
Лo
ON
Distance Downrange
Submit
Request Answer
initial position
(x- Yo
<Return to Assignment
Provide Feedback
Height
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 7 steps with 6 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Recommended textbooks for you

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

College Physics
Physics
ISBN:
9781938168000
Author:
Paul Peter Urone, Roger Hinrichs
Publisher:
OpenStax College

University Physics Volume 1
Physics
ISBN:
9781938168277
Author:
William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:
OpenStax - Rice University

Physics for Scientists and Engineers, Technology …
Physics
ISBN:
9781305116399
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

College Physics
Physics
ISBN:
9781938168000
Author:
Paul Peter Urone, Roger Hinrichs
Publisher:
OpenStax College

Principles of Physics: A Calculus-Based Text
Physics
ISBN:
9781133104261
Author:
Raymond A. Serway, John W. Jewett
Publisher:
Cengage Learning

Glencoe Physics: Principles and Problems, Student…
Physics
ISBN:
9780078807213
Author:
Paul W. Zitzewitz
Publisher:
Glencoe/McGraw-Hill

College Physics
Physics
ISBN:
9781285737027
Author:
Raymond A. Serway, Chris Vuille
Publisher:
Cengage Learning