Content Blackboard Learn +AddThis Social Bookn an Mail Taylor, Makayla s G what are list publicatinat OOhttps://elearning.kctcs.edu/ultra/courses/493523760 1/cl/outline 90% The following table shows the length, in meters, of the winning long jump in the Olympic Games for the indicated year. (One meter is 39.37 inches.) Year 1900 1904 1908 1912 Length 7.19 7.34 7.48 7.60 (a) Find the equation of the regression line that gives the length as a function of time. (Lett be the number of years since 1900 and L the length of the wining long jump, in meters. Round the regression line parameters to three decimal places.) L(t) - x (b) Explain in practical terms the meaning of the slope of the regression line. In practical terms the meaning of the slope, 14 meter per year, of the regression line is that each year the length of the winning long jump increased by an x average of 14 meter, or about 14 X inches. (c) Plot the data points and the regression line. L L 7.7 7.7 7.6 7.6 7.5 7.5 7.4 7.4 7.3 7.3 7.2 72 7.1 F 8 12 4 12 e e here to search 7:02 PM 10/10/2019 II X
Content Blackboard Learn +AddThis Social Bookn an Mail Taylor, Makayla s G what are list publicatinat OOhttps://elearning.kctcs.edu/ultra/courses/493523760 1/cl/outline 90% The following table shows the length, in meters, of the winning long jump in the Olympic Games for the indicated year. (One meter is 39.37 inches.) Year 1900 1904 1908 1912 Length 7.19 7.34 7.48 7.60 (a) Find the equation of the regression line that gives the length as a function of time. (Lett be the number of years since 1900 and L the length of the wining long jump, in meters. Round the regression line parameters to three decimal places.) L(t) - x (b) Explain in practical terms the meaning of the slope of the regression line. In practical terms the meaning of the slope, 14 meter per year, of the regression line is that each year the length of the winning long jump increased by an x average of 14 meter, or about 14 X inches. (c) Plot the data points and the regression line. L L 7.7 7.7 7.6 7.6 7.5 7.5 7.4 7.4 7.3 7.3 7.2 72 7.1 F 8 12 4 12 e e here to search 7:02 PM 10/10/2019 II X
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
ChapterP: Prologue: Calculator Arithmetic
Section: Chapter Questions
Problem 1E: Valentines Day According to the National Retail Federation, on Valentines Day 2015, American men...
Related questions
Question
what are the blanks
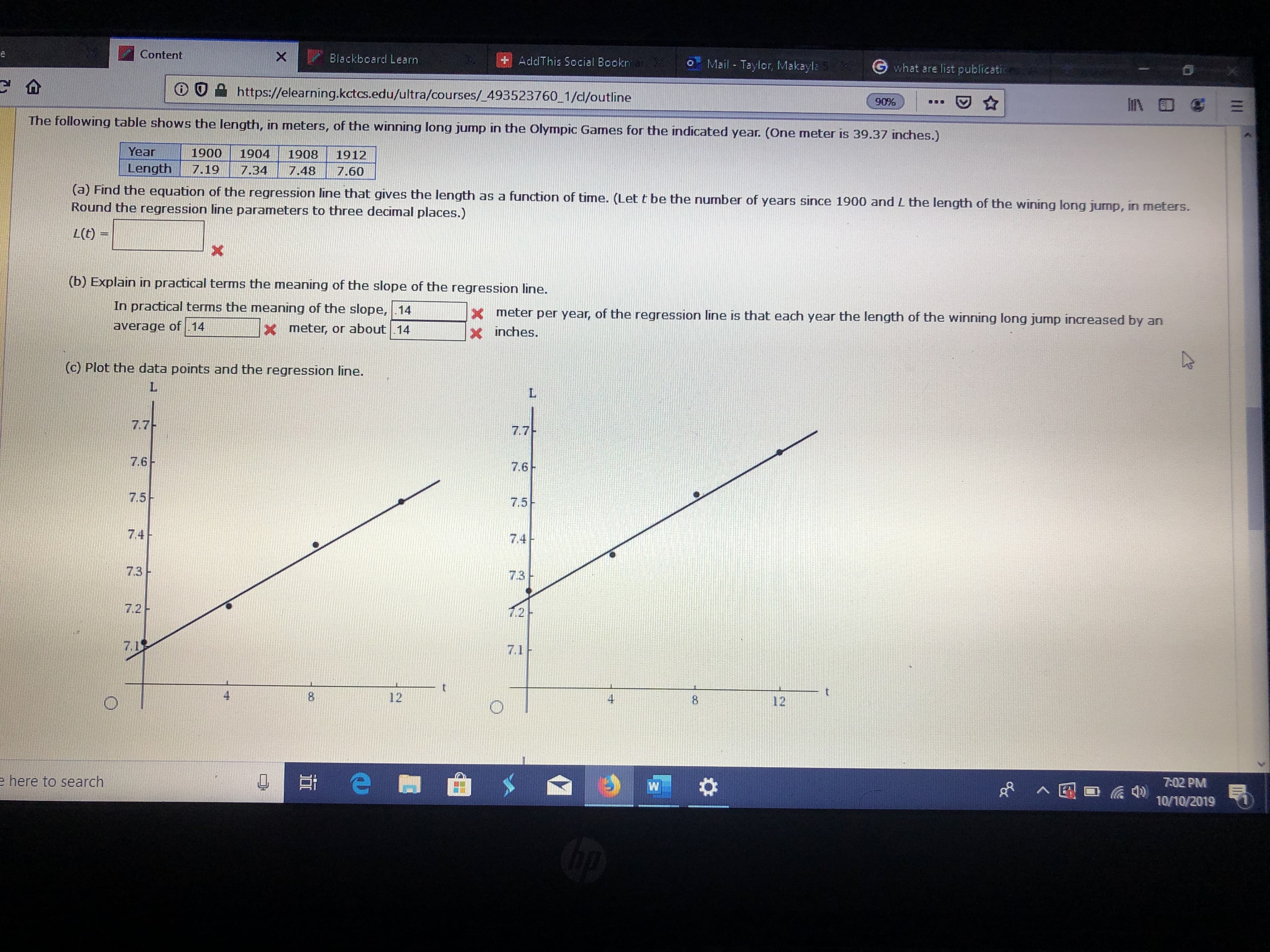
Transcribed Image Text:Content
Blackboard Learn
+AddThis Social Bookn an
Mail Taylor, Makayla s
G what are list publicatinat
OOhttps://elearning.kctcs.edu/ultra/courses/493523760 1/cl/outline
90%
The following table shows the length, in meters, of the winning long jump in the Olympic Games for the indicated year. (One meter is 39.37 inches.)
Year
1900
1904
1908
1912
Length
7.19
7.34
7.48
7.60
(a) Find the equation of the regression line that gives the length as a function of time. (Lett be the number of years since 1900 and L the length of the wining long jump, in meters.
Round the regression line parameters to three decimal places.)
L(t) -
x
(b) Explain in practical terms the meaning of the slope of the regression line.
In practical terms the meaning of the slope, 14
meter per year, of the regression line is that each year the length of the winning long jump increased by an
x
average of 14
meter, or about 14
X inches.
(c) Plot the data points and the regression line.
L
L
7.7
7.7
7.6
7.6
7.5
7.5
7.4
7.4
7.3
7.3
7.2
72
7.1 F
8
12
4
12
e
e here to search
7:02 PM
10/10/2019
II
X
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill

Big Ideas Math A Bridge To Success Algebra 1: Stu…
Algebra
ISBN:
9781680331141
Author:
HOUGHTON MIFFLIN HARCOURT
Publisher:
Houghton Mifflin Harcourt

Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL