Definition: Let f be a real-valued function of a real variable and let M be any real number. The function Mf, called the multiple of f by M or M times f, is the real-valued function with the same domain as f that is defined by the rule Mf(x) = M(f(x)) for each x in the domain of f. Assume that f is a real-valued function of a real variable, and prove the following statement. If f is increasing on a set S and if M is any negative real number, then Mf is decreasing on S. function on a set S of real numbers, and suppose M is any negative Proof: Suppose f is any increasing number. [We will show that Mf is decreasing on S.] Let x₁ and x₂ be any real numbers in S such that x₁ < x₂. Since f is increasing on S, f(x₁)< f(x₂). Multiplying both sides by M gives that M(xi) negative X M(x₁) ---Select--- -f(x₁) M(x₁) M(f(x)) M(x₂) X because M is --Select--- ---Select--- -f(x₁) -f(x=) M(x1) M(x₂) M(f(x:)) M(f(x=)) V By definition of Mf, (MF)(x₁) = ---Select--- and (MF) (x₂) = Thus, by substitution, (Mf)(x₁) * (MF) (x₂). Since x₁ and x₂ were arbitrarily chosen real numbers in S such that x₁ < x₂, we can conclude that Mf is decreasing on S. V real
Definition: Let f be a real-valued function of a real variable and let M be any real number. The function Mf, called the multiple of f by M or M times f, is the real-valued function with the same domain as f that is defined by the rule Mf(x) = M(f(x)) for each x in the domain of f. Assume that f is a real-valued function of a real variable, and prove the following statement. If f is increasing on a set S and if M is any negative real number, then Mf is decreasing on S. function on a set S of real numbers, and suppose M is any negative Proof: Suppose f is any increasing number. [We will show that Mf is decreasing on S.] Let x₁ and x₂ be any real numbers in S such that x₁ < x₂. Since f is increasing on S, f(x₁)< f(x₂). Multiplying both sides by M gives that M(xi) negative X M(x₁) ---Select--- -f(x₁) M(x₁) M(f(x)) M(x₂) X because M is --Select--- ---Select--- -f(x₁) -f(x=) M(x1) M(x₂) M(f(x:)) M(f(x=)) V By definition of Mf, (MF)(x₁) = ---Select--- and (MF) (x₂) = Thus, by substitution, (Mf)(x₁) * (MF) (x₂). Since x₁ and x₂ were arbitrarily chosen real numbers in S such that x₁ < x₂, we can conclude that Mf is decreasing on S. V real
College Algebra (MindTap Course List)
12th Edition
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:R. David Gustafson, Jeff Hughes
Chapter3: Functions
Section3.3: More On Functions; Piecewise-defined Functions
Problem 98E: Determine if the statemment is true or false. If the statement is false, then correct it and make it...
Related questions
Question
100%
I struggle the most starting from "Multiplying both sides by M gives that..." and below
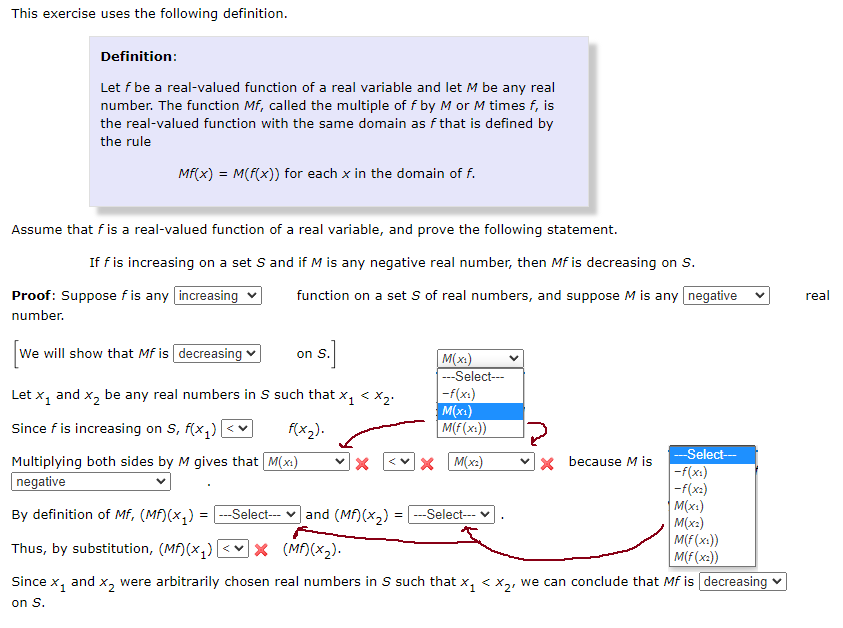
Transcribed Image Text:This exercise uses the following definition.
Definition:
Let f be a real-valued function of a real variable and let M be any real
number. The function Mf, called the multiple of f by M or M times f, is
the real-valued function with the same domain as f that is defined by
the rule
Mf(x) = M(f(x)) for each x in the domain of f.
Assume that f is a real-valued function of a real variable, and prove the following statement.
If f is increasing on a set S and if M is any negative real number, then Mf is decreasing on S.
function on a set S of real numbers, and suppose M is any negative
Proof: Suppose f is any increasing
number.
We will show that Mf is decreasing
Let x₁ and x₂ be any real numbers in S such that X₁ < x₂.
Since f is increasing on S, f(x₁)<
f(x₂).
Multiplying both sides by M gives that M(x₁)
negative
on S.
M(x₁)
---Select---
-f(x:)
M(x₁)
M(f(x:))
X M(x₂)
and (Mf)(x₂) = ---Select--- ♥
because M is
---Select---
-f(x₁)
-f(x₂)
M(x1)
M(x₂)
By definition of Mf, (Mf)(x₁) = ---Select---
Thus, by substitution, (Mf)(x₁) < * (MF) (x₂).
Since x₁ and x₂ were arbitrarily chosen real numbers in S such that X₁ < x₂, we can conclude that Mf is decreasing
on S.
M(f(x:))
M(f(x₂))
real
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage



Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill