Homework Help is Here – Start Your Trial Now!
Math
Calculus
EXAMPLE 1 Air is being pumped into a spherical balloon so that its volume increases at a rate of 200 cm/s. How fast is the radius of the balloon increasing when the diameter is 20 cm? SOLUTION We start by identifying two things: the given information: The rate of increase of the volume of air is 200 cm /s. and the unknown: The rate of increase of the radius when the diameter is 20 cm. In order to express these quantities mathematically, we introduce some suggestive notation: Let V be the volume of the balloon and let r be its radius. The key thing to remember is that rates of change are derivatives. In this problem, the volume and the radius are both functions of the time. The rate of increase of the volume with respect to time is the derivative dv/dt, and the rate of increase of the radius is dr/dt. We can therefore restate the given and the unknown as follows: dv = 200 cm3/s dt Given: dr dt Unknown: when r = cm. In order to connect dV/dt and dr/dt, we first relate V and r by the formula for the volume of a sphere: v= Tr. In order to use the given information, we differentiate each side of this equation with respect to t. To differentiate the right side, we need to use the Chain Rule: dv - dv dr dr dt dr dt dt Now we solve for the unknown quantity: dr dt dv dt

EXAMPLE 1 Air is being pumped into a spherical balloon so that its volume increases at a rate of 200 cm/s. How fast is the radius of the balloon increasing when the diameter is 20 cm? SOLUTION We start by identifying two things: the given information: The rate of increase of the volume of air is 200 cm /s. and the unknown: The rate of increase of the radius when the diameter is 20 cm. In order to express these quantities mathematically, we introduce some suggestive notation: Let V be the volume of the balloon and let r be its radius. The key thing to remember is that rates of change are derivatives. In this problem, the volume and the radius are both functions of the time. The rate of increase of the volume with respect to time is the derivative dv/dt, and the rate of increase of the radius is dr/dt. We can therefore restate the given and the unknown as follows: dv = 200 cm3/s dt Given: dr dt Unknown: when r = cm. In order to connect dV/dt and dr/dt, we first relate V and r by the formula for the volume of a sphere: v= Tr. In order to use the given information, we differentiate each side of this equation with respect to t. To differentiate the right side, we need to use the Chain Rule: dv - dv dr dr dt dr dt dt Now we solve for the unknown quantity: dr dt dv dt

Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
10th Edition
ISBN:9781337278461
Author:Ron Larson
Publisher:Ron Larson
Chapter6: Topics In Analytic Geometry
Section: Chapter Questions
Problem 33CT
See similar textbooks
icon
Related questions
Question
If we put r= 10 and dV/dt = 200 in this equation, we obtain 1 dr dt 200 = The radius of the balloon is increasing at the rate of cm/s (rounded to four decimal places).
Transcribed Image Text:If we put r= 10 and dV/dt = 200 in this equation, we obtain 1 dr dt 200 = The radius of the balloon is increasing at the rate of cm/s (rounded to four decimal places).
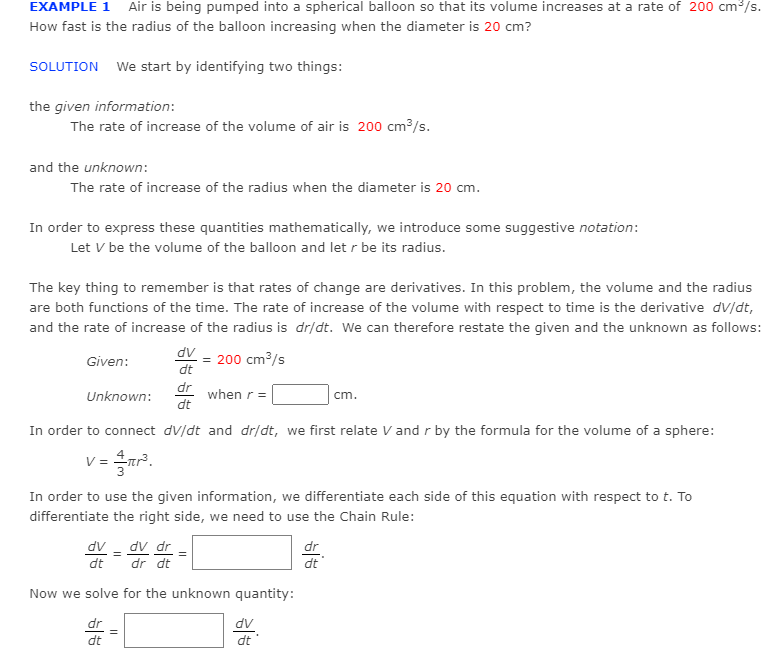
EXAMPLE 1 Air is being pumped into a spherical balloon so that its volume increases at a rate of 200 cm/s. How fast is the radius of the balloon increasing when the diameter is 20 cm? SOLUTION We start by identifying two things: the given information: The rate of increase of the volume of air is 200 cm /s. and the unknown: The rate of increase of the radius when the diameter is 20 cm. In order to express these quantities mathematically, we introduce some suggestive notation: Let V be the volume of the balloon and let r be its radius. The key thing to remember is that rates of change are derivatives. In this problem, the volume and the radius are both functions of the time. The rate of increase of the volume with respect to time is the derivative dv/dt, and the rate of increase of the radius is dr/dt. We can therefore restate the given and the unknown as follows: dv = 200 cm3/s dt Given: dr dt Unknown: when r = cm. In order to connect dV/dt and dr/dt, we first relate V and r by the formula for the volume of a sphere: v= Tr. In order to use the given information, we differentiate each side of this equation with respect to t. To differentiate the right side, we need to use the Chain Rule: dv - dv dr dr dt dr dt dt Now we solve for the unknown quantity: dr dt dv dt
Transcribed Image Text:EXAMPLE 1 Air is being pumped into a spherical balloon so that its volume increases at a rate of 200 cm/s. How fast is the radius of the balloon increasing when the diameter is 20 cm? SOLUTION We start by identifying two things: the given information: The rate of increase of the volume of air is 200 cm /s. and the unknown: The rate of increase of the radius when the diameter is 20 cm. In order to express these quantities mathematically, we introduce some suggestive notation: Let V be the volume of the balloon and let r be its radius. The key thing to remember is that rates of change are derivatives. In this problem, the volume and the radius are both functions of the time. The rate of increase of the volume with respect to time is the derivative dv/dt, and the rate of increase of the radius is dr/dt. We can therefore restate the given and the unknown as follows: dv = 200 cm3/s dt Given: dr dt Unknown: when r = cm. In order to connect dV/dt and dr/dt, we first relate V and r by the formula for the volume of a sphere: v= Tr. In order to use the given information, we differentiate each side of this equation with respect to t. To differentiate the right side, we need to use the Chain Rule: dv - dv dr dr dt dr dt dt Now we solve for the unknown quantity: dr dt dv dt
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 2 steps with 2 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning
College Algebra
College Algebra
Algebra
ISBN:
9781337282291
Author:
Ron Larson
Publisher:
Cengage Learning
Linear Algebra: A Modern Introduction
Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning
Functions and Change: A Modeling Approach to Coll…
Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS