EXAMPLE 3 The density at any point on a semicircular lamina is proportional to the distance from the center of the circle. Find the center of mass of the lamina. ²+ y = a² SOLUTION Let's place the lamina as the upper half of the circle x? + y2 = a?. (See the figure.) Then the distance from a point (x, y) to the center of the circle (0.) (the origin) is Vx? + y². Therefore the density function is P(x, y) = KV + y? -a Video Example () where K is some constant. Both the density function and the shape of the lamina suggest that we convert to polar coordinates. Then Vx2 + y2 = r and the region D is given by 0
EXAMPLE 3 The density at any point on a semicircular lamina is proportional to the distance from the center of the circle. Find the center of mass of the lamina. ²+ y = a² SOLUTION Let's place the lamina as the upper half of the circle x? + y2 = a?. (See the figure.) Then the distance from a point (x, y) to the center of the circle (0.) (the origin) is Vx? + y². Therefore the density function is P(x, y) = KV + y? -a Video Example () where K is some constant. Both the density function and the shape of the lamina suggest that we convert to polar coordinates. Then Vx2 + y2 = r and the region D is given by 0
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section4.6: Variation
Problem 33E
Related questions
Question
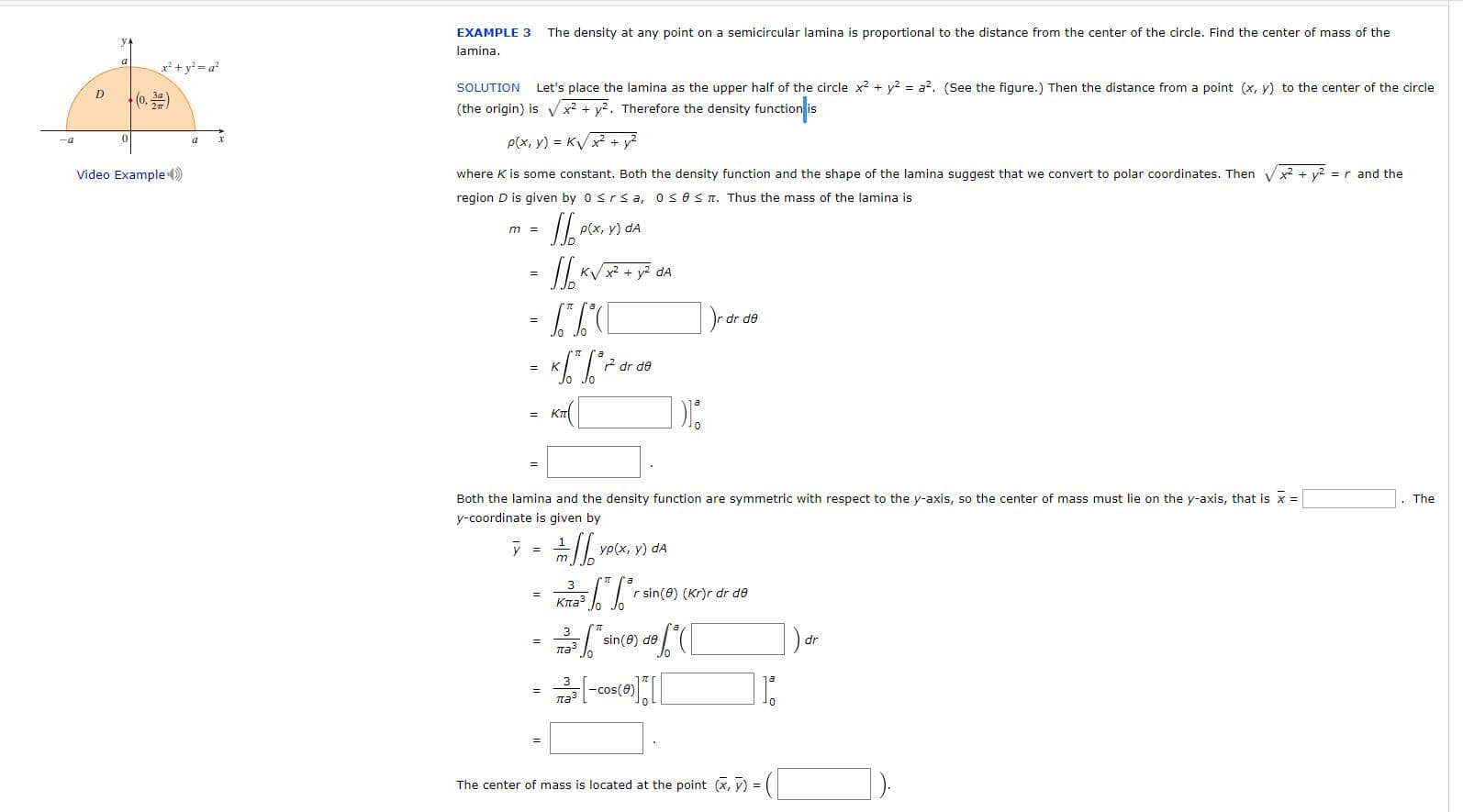
Transcribed Image Text:EXAMPLE 3
The density at any point on a semicircular lamina is proportional to the distance from the center of the circle. Find the center of mass of the
lamina.
²+ y = a²
SOLUTION
Let's place the lamina as the upper half of the circle x? + y2 = a?. (See the figure.) Then the distance from a point (x, y) to the center of the circle
(0.)
(the origin) is Vx? + y². Therefore the density function is
P(x, y) = KV + y?
-a
Video Example ()
where K is some constant. Both the density function and the shape of the lamina suggest that we convert to polar coordinates. Then Vx2 + y2 = r and the
region D is given by 0 <rs a, osesn. Thus the mass of the lamina is
P(x, y) dA
- ea
KV + y? dA
de
2 dr de
Кп
Both the lamina and the density function are symmetric with respect to the y-axis, so the center of mass must lie on the y-axis, that is x =
. The
y-coordinate is given by
yρ(x, y ) dA
r sin(0) (Kr)r dr de
Кла
3
sin(e) de
паз
-cos(0)
na
The center of mass is located at the point (x, y) =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 5 images

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage