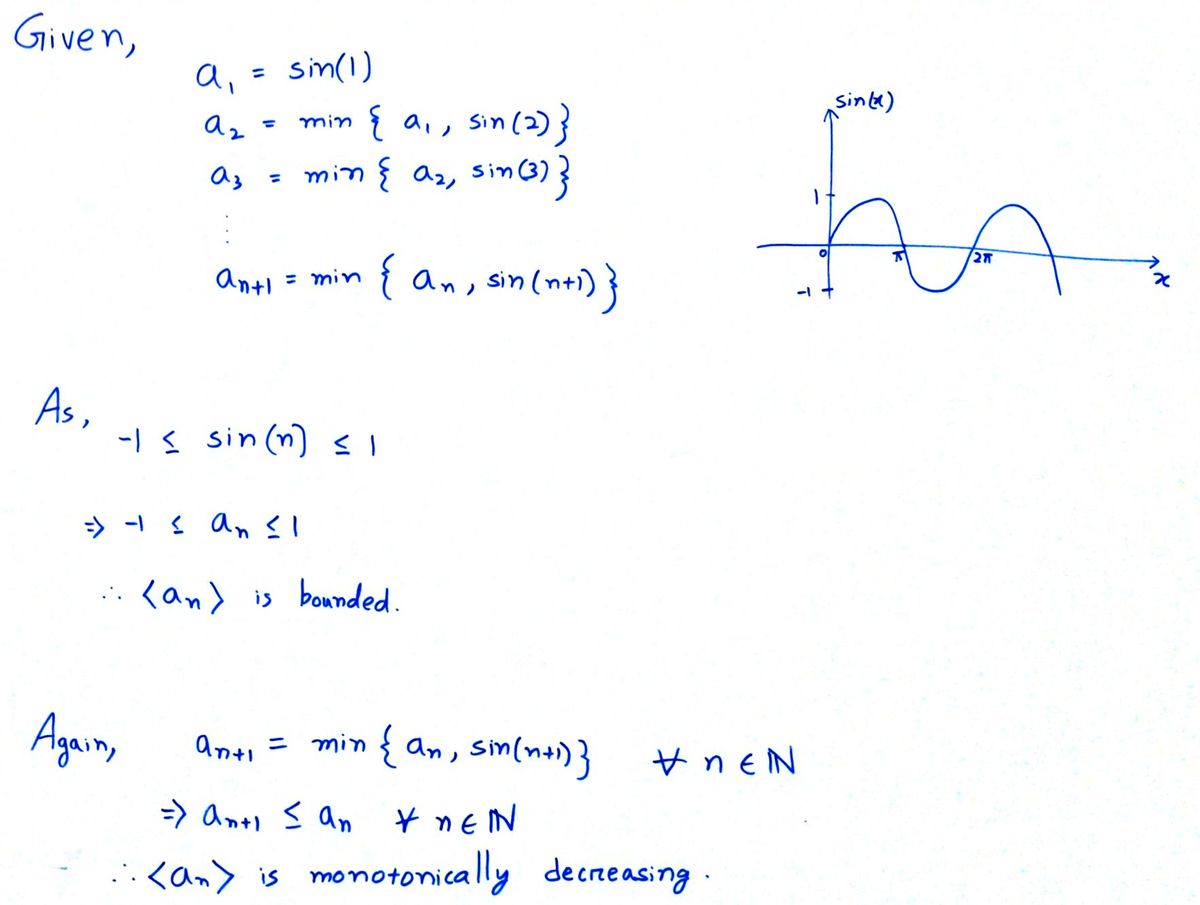
EXERCISE 7: Sequence: The first term of a sequence is a1 = sin(1). The next terms are: a2 = min{a1,sin(2)} (the smallest of a1 and sin 2), az = min{a2, sin(3)} (the smallest of az and sin 3),... an+1 = min{an, sin(n + 1)} (the smallest of an and sin(n +1)). Is this sequence {an} converging or diverging?
EXERCISE 7: Sequence: The first term of a sequence is a1 = sin(1). The next terms are: a2 = min{a1,sin(2)} (the smallest of a1 and sin 2), az = min{a2, sin(3)} (the smallest of az and sin 3),... an+1 = min{an, sin(n + 1)} (the smallest of an and sin(n +1)). Is this sequence {an} converging or diverging?
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter10: Sequences, Series, And Probability
Section: Chapter Questions
Problem 2RE
Related questions
Topic Video
Question

Transcribed Image Text:EXERCISE 7: Sequence: The first term of a sequence is a1 = sin(1). The next terms are:
a2 = min{a1,sin(2)} (the smallest of a1 and sin 2),
az = min{a2, sin(3)} (the smallest of az and sin 3),...
an+1 = min{an, sin(n + 1)} (the smallest of an and sin(n +1)).
Is this sequence {an} converging or diverging?
Expert Solution
Step 1
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage