Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: adapted from The Celebrated Jumping Frog of Calaveras Countyby Mark Twain I found Simon Wheeler…
A: The objective of the question is to match the details from the passage with the statements that best…
Q: 2. Which of the following simplifies to -1? А. I В. 2 c. ³ D. A
A: We have to simplify
Q: value(s) and identiry the rejection region The critical value(s) is/are. (Round to three decimal…
A:
Q: Given the following matrix equation, which of the following is the correct matrix solution, A? -5 5…
A: The given matrix,A=0.6-552-416+0.5-215-7315
Q: I need the correct answer for the above question whose reverse is not correct.
A: There are four statements.  All four are if - then statements * if A then B ( means if event A…
Q: Match the following graph to its inverse. -5-4-3-2 5 3 ↑ M T + 1 2 3 4 5
A:
Q: 1. Find x and y yo 35
A:
Q: i need help with the following question
A: Step 1: Step 2: Step 3: Step 4:
Q: 9. Which of the following expresses 37-2/28 in simplest form? -/21 d. -7 а. -1 с. b. -57
A:
Q: adapted from The Celebrated Jumping Frog of Calaveras Countyby Mark Twain I found Simon Wheeler…
A: The objective of the question is to match the details from the passage with the statements that best…
Q: A = 0 -1 3 -7 0-5 4 7 1 0 -2 -10 0 10 6 12
A:
Q: Compute the following equation 2 -1 4 3 1 4 2 2 9 0 -1 - 1 0 1
A: The given matrix operation,The aim is to find the given matrix multiplication.
Q: Which of the following expresses-2/15 x 4/6 in simplest form? a. -12 /10 b. -24/10 8. c. -72/10 d.…
A: Simplest form will be
Q: Graph the solution set of the follo 2x-y > 2x+ y > 5
A:
Q: Hello, the answers provided were incorrect.
A: From given  mean is 0 and standard deviation is 1
Q: ot clear to me how did you find questio
A: Given: Mean years of service = 14.88889
Q: 123 30 Find the values of x and y. Write your answers in simplest form.
A:
Q: One question with parts ...
A: In the given case, the appropriate hypothesis is given by  H0: p = 0.5H1: p > 0.5 where p is the…
Q: 10 3 - 4i O 1.2 - 1.6i O 1.6 + 1.2i O 1.2 + 1.6i O 1.6 - 1.2i
A: 1.2 + 1.6 i
Q: 1. Ф(8) Answer: Show your work or explain your reasoning here:
A:
bartleby

Concept explainers

Statements and Logic
Logic is the analysis of general patterns of thoughts without regard to any specific sense of context.
Topic Video
Question

Need answer to the following question.

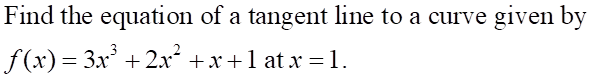
Find the equation of a tangent line to a curve given by f(x) = 3x3 + 2x2 +x+1at x =1.
expand button
Transcribed Image Text:Find the equation of a tangent line to a curve given by f(x) = 3x3 + 2x2 +x+1at x =1.
Expert Solution
Check Mark
Step 1

We first find the slope of the tangent for which we need derivative of f(x).  Differentiating f(x) w.r.t. x we get:

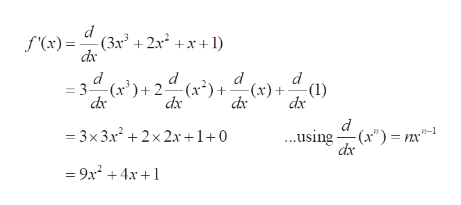
Calculus homework question answer, Step 1, Image 1
expand button
Step 2

Now, slope is the value of f’(x) at the given point x = 1.

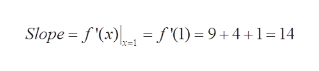
Calculus homework question answer, Step 2, Image 1
expand button
Step 3

Now, to find any one point on the tangent line, we consider the fact that tangent line is drawn at x=1. This point also lies on the curve and hence its y-coordinate is the value of f(x) at x=1. We get:

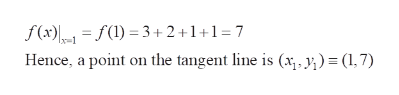
Calculus homework question answer, Step 3, Image 1
expand button
bartleby

Trending nowThis is a popular solution!

bartleby

Step by stepSolved in 5 steps with 5 images

Blurred answer
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS