Finding an Equation of a Tangent Line In Exercis and 62, find equations of the two tangent lines to the grap Approximating a Deri evaluate f(2) and f(2.1) and f that pass through the indicated point. 62. f(x) = x2 61. f(x) = 4x- x2 67. f(x) = x(4 - x y у Using the Derivative 10 (2, 5) 8 6 4 alternative fe 3 45 6 78 4 derivative at 3+ wwwe 2 y 69. f(x) = x3 + 2x2 + 1, -6-4 -2 2 4 6 70. g(x) = x2 - x, c = 1 -X RI,-3) -4 5 1 2 3 71. g(x) = x, c = 0 f A 63. Graphical Reasoning Use a each function and its tangent lines at x = -1, x = x =1. Based on the results, determine whether the slane tangent lines to the graph of a fanction at different values always distinct. graphing utility to 73. f(x) = (x - 6)2/3, c x 75. h(x) = lx +7|, c = C 1 2 3 Determir 77-80, de are differentia (b) g(x) = (a) f(x) x TY f(x)(x + 4)2/3 a function how you HOW DO YOU SEE IT? The figuré shows the graph of g'. 64. function Explain +t always -6 -4 -2 4 2+ nmetric metric 79, f(r -6-4 ob 151
Finding an Equation of a Tangent Line In Exercis and 62, find equations of the two tangent lines to the grap Approximating a Deri evaluate f(2) and f(2.1) and f that pass through the indicated point. 62. f(x) = x2 61. f(x) = 4x- x2 67. f(x) = x(4 - x y у Using the Derivative 10 (2, 5) 8 6 4 alternative fe 3 45 6 78 4 derivative at 3+ wwwe 2 y 69. f(x) = x3 + 2x2 + 1, -6-4 -2 2 4 6 70. g(x) = x2 - x, c = 1 -X RI,-3) -4 5 1 2 3 71. g(x) = x, c = 0 f A 63. Graphical Reasoning Use a each function and its tangent lines at x = -1, x = x =1. Based on the results, determine whether the slane tangent lines to the graph of a fanction at different values always distinct. graphing utility to 73. f(x) = (x - 6)2/3, c x 75. h(x) = lx +7|, c = C 1 2 3 Determir 77-80, de are differentia (b) g(x) = (a) f(x) x TY f(x)(x + 4)2/3 a function how you HOW DO YOU SEE IT? The figuré shows the graph of g'. 64. function Explain +t always -6 -4 -2 4 2+ nmetric metric 79, f(r -6-4 ob 151
Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)
6th Edition
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Bruce Crauder, Benny Evans, Alan Noell
Chapter2: Graphical And Tabular Analysis
Section2.6: Optimization
Problem 11E: Maximum Sales Growth This is a continuation of Exercise 10. In this exercise, we determine how the...
Related questions
Concept explainers
Contingency Table
A contingency table can be defined as the visual representation of the relationship between two or more categorical variables that can be evaluated and registered. It is a categorical version of the scatterplot, which is used to investigate the linear relationship between two variables. A contingency table is indeed a type of frequency distribution table that displays two variables at the same time.
Binomial Distribution
Binomial is an algebraic expression of the sum or the difference of two terms. Before knowing about binomial distribution, we must know about the binomial theorem.
Topic Video
Question
61
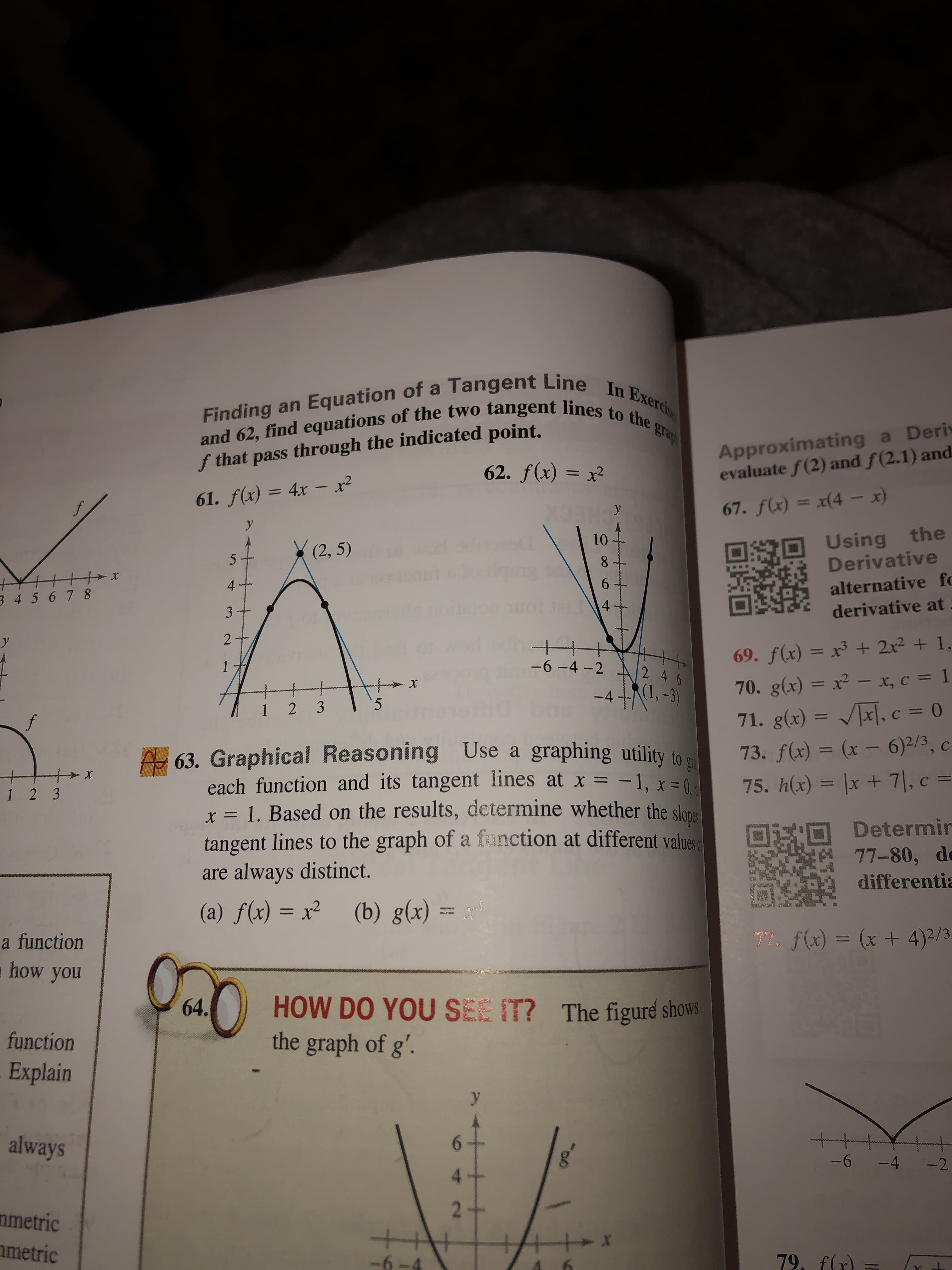
Transcribed Image Text:Finding an Equation of a Tangent Line In Exercis
and 62, find equations of the two tangent lines to the grap
Approximating a Deri
evaluate f(2) and f(2.1) and
f that pass through the indicated point.
62. f(x) = x2
61. f(x) = 4x- x2
67. f(x) = x(4 - x
y
у
Using the
Derivative
10
(2, 5)
8
6
4
alternative fe
3 45 6 78
4
derivative at
3+
wwwe
2
y
69. f(x) = x3 + 2x2 + 1,
-6-4 -2
2 4 6
70. g(x) = x2 - x, c = 1
-X
RI,-3)
-4
5
1 2 3
71. g(x) = x, c = 0
f
A 63. Graphical Reasoning Use a
each function and its tangent lines at x = -1, x =
x =1. Based on the results, determine whether the slane
tangent lines to the graph of a fanction at different values
always distinct.
graphing utility to
73. f(x) = (x - 6)2/3, c
x
75. h(x) = lx +7|, c =
C
1 2 3
Determir
77-80, de
are
differentia
(b) g(x) =
(a) f(x) x
TY f(x)(x + 4)2/3
a function
how you
HOW DO YOU SEE IT? The figuré shows
the graph of g'.
64.
function
Explain
+t
always
-6
-4
-2
4
2+
nmetric
metric
79, f(r
-6-4
ob
151
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning

Functions and Change: A Modeling Approach to Coll…
Algebra
ISBN:
9781337111348
Author:
Bruce Crauder, Benny Evans, Alan Noell
Publisher:
Cengage Learning