Generalize Theorem 1.3.9 by proving that every rational solution of a polyno- mial equation x" + an-1a"-1 + + a1x + = 0, | with integer coefficients ak, is an integer solution.
Generalize Theorem 1.3.9 by proving that every rational solution of a polyno- mial equation x" + an-1a"-1 + + a1x + = 0, | with integer coefficients ak, is an integer solution.
Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter4: Polynomial And Rational Functions
Section4.2: Properties Of Division
Problem 51E
Related questions
Question
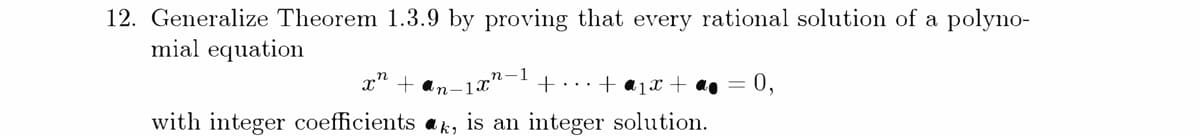
Transcribed Image Text:12. Generalize Theorem 1.3.9 by proving that every rational solution of a polyno-
mial equation
-1x"-1
+ «1x + a• = 0,
+...
with integer coefficients a k,
is an integer solution.

Transcribed Image Text:Theorem 1.3.9. If k is an integer and the equation x = k has a rational solution,
then that solution is actually an integer.
Proof. Suppose r is a ratiomal number such that r2 = k. Let r =
as a fraction in which n and m have no common factors. Then,
er expressed
2
n
k
and so n? = m²k.
m
This equationm implies that m divides n2. However, if m 7 1, then m can be
expressed as a product of primes, and each of these primes must also divide n2.
However, if a prime number divides n2, it must also divide n (Exercise 1.3.14).
Thus, each prime factor of m divides n. Since n and m have no common factors,
this is impossible. We conclude that m =
1 and, hence, that r = n is an integer.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps

Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

Elements Of Modern Algebra
Algebra
ISBN:
9781285463230
Author:
Gilbert, Linda, Jimmie
Publisher:
Cengage Learning,

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning