Algebra and Trigonometry (MindTap Course List)
4th Edition
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:James Stewart, Lothar Redlin, Saleem Watson
Chapter2: Functions
Section2.4: Average Rate Of Change Of A Function
Problem 4.2E: bThe average rate of change of the linear function f(x)=3x+5 between any two points is ________.
Related questions
Question
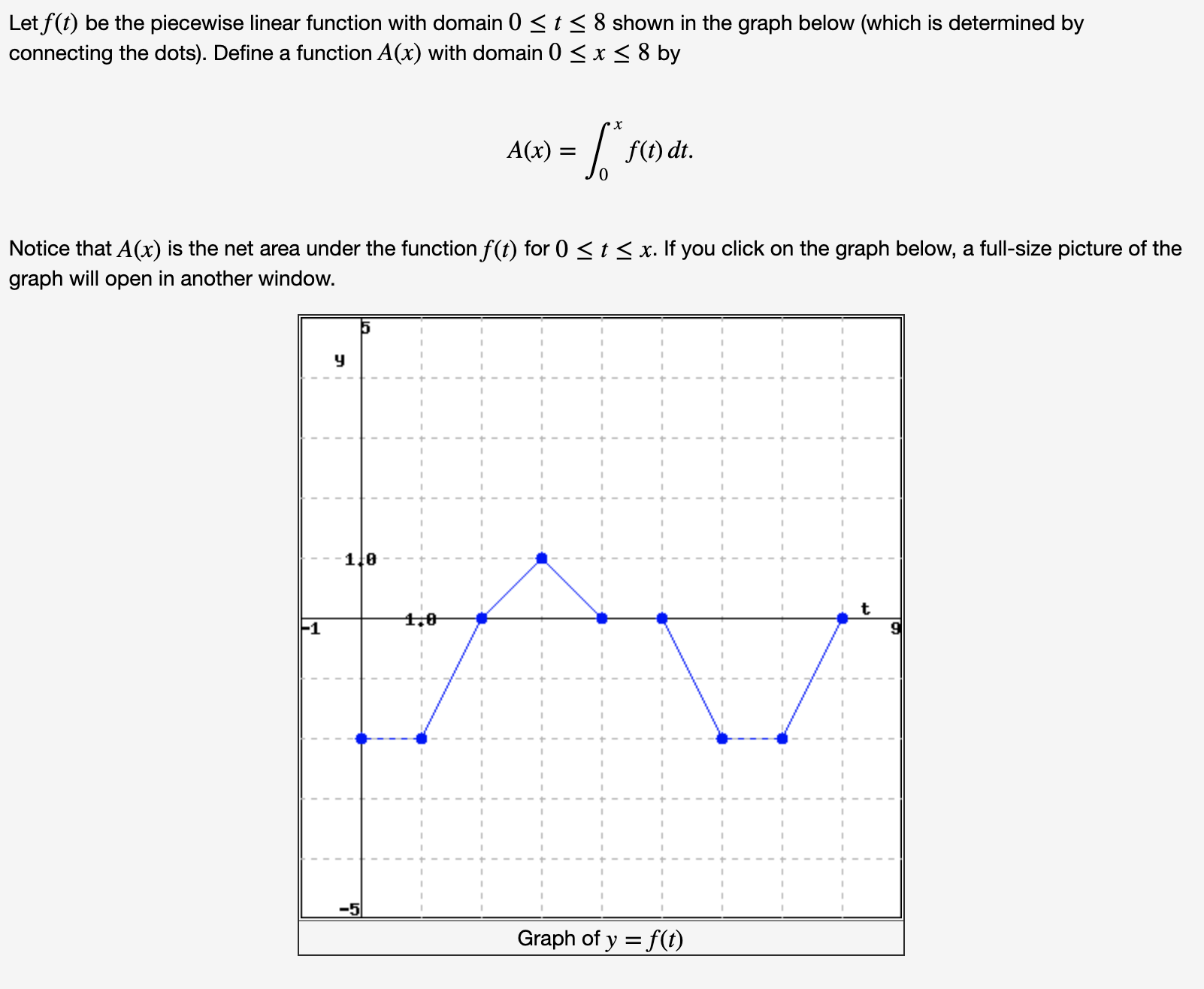
Transcribed Image Text:Let f(t) be the piecewise linear function with domain 0 <t < 8 shown in the graph below (which is determined by
connecting the dots). Define a function A(x) with domain 0 <x < 8 by
:| f(1) dt.
A(x)
Notice that A(x) is the net area under the function f(t) for 0 < t < x. If you click on the graph below, a full-size picture of the
graph will open in another window.
1.0
4,0
F1
-5
Graph of y = f(t)

Transcribed Image Text:(A) Find the following values of the function A(x).
A(0) =
A(1) =
A(2) =
A(3) =
A(4) =
A(5) =
A(6) =
A(7) =
A(8) =
(B) Use interval notation to indicate the interval or union of intervals where A(x) is increasing and decreasing.
A(x) is increasing for x in the interval
A(x) is decreasing for x in the interval
(C) Find where A(x) has its maximum and minimum values.
A(x) has its maximum value when x =
A(x) has its minimum value when x =
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 4 images

Recommended textbooks for you

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra for College Students
Algebra
ISBN:
9781285195780
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning