Problem 2. Suppose out of 50 tables in a restaurant, 35 have a person who ordered with his/her entree, 25 have a person who ordered salad with his/her entree, and 10 have ordered both. soup (a) How many tables will have neither a soup nor a salad delivered to them? (b) How many tables will only have a salad delivered? (c) What is the probability that a table will have a soup or a salad delivered? (d) What is the probability that a table will not have a soup delivered? (e) Are the events "soup delivered to the table" and "salad delivered to the table" mutu- ally exclusive? Are they independent? Justify your answers.
Permutations and Combinations
If there are 5 dishes, they can be relished in any order at a time. In permutation, it should be in a particular order. In combination, the order does not matter. Take 3 letters a, b, and c. The possible ways of pairing any two letters are ab, bc, ac, ba, cb and ca. It is in a particular order. So, this can be called the permutation of a, b, and c. But if the order does not matter then ab is the same as ba. Similarly, bc is the same as cb and ac is the same as ca. Here the list has ab, bc, and ac alone. This can be called the combination of a, b, and c.
Counting Theory
The fundamental counting principle is a rule that is used to count the total number of possible outcomes in a given situation.
Could you do question 2, d and e?

Given data
Total tables n(T)= 50
No of persons who ordered soup, n(A) = 35
No of persons who ordered salad, n(B) = 25
No of persons who ordered both, n(A∩B) = 10
d)
Probability that the table will not have a soup delivered is given by
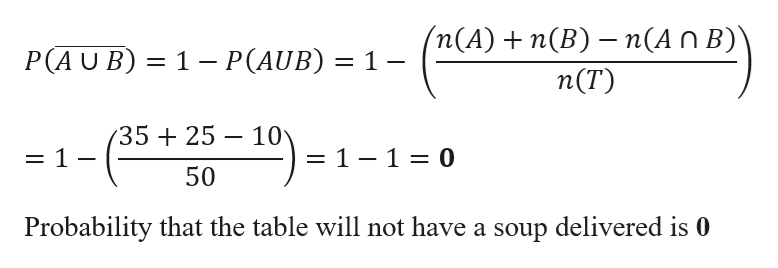
e)
For events to be mutually exclusive
n(A∩B) = 0 and P(AUB)=P(A)+P(B)
In the given problem
n(A∩B) ≠ 0
So, the events soup delivered to the table and salad delivered to the table are not mutually exclusive
For the events to be independent,
P(A∩B) = P(A) × P(B)
P(A) = 35/50 = 0.7
P(B) = 25/50 = 0.5
P(A∩B) = 10/50= 0.2
P(A) × P(B) = 0.7 × 0.5 = 0.35
This shows that
P(A∩B) ≠ P(A) × P(B)
So, the given events are not independent
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 1 images


