Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
Chapter10: Analytic Geometry
Section10.6: The Three-dimensional Coordinate System
Problem 41E: Does the sphere x2+y2+z2=100 have symmetry with respect to the a x-axis? b xy-plane?
Related questions
Question
9- 15-6
![•√ √ F(x₂:
Evaluate
f(x, y, z) ds.
f(x, y, z)= √√√x² + y² + z²
S: z = √√√x² + y², (x - 1)² + y² ≤ 1
Part 1 of 6
Find the surface integral using the formula
2) ds = √ √₁²
116FX
Here, g(x, y) = Z = √x² + y². Find the partial derivatives gx(x, y) and g(x, y).
f(x, y, z) ds
gx(x, y)
gy(x, y)
X
y
f(x, y, g(x, y))√1 + [9x (x, y)]²+ [gy (x, y)]² dA.
Part 2 of 6
Substitute these partial derivatives into
1 + [9x (x, y)]²+ [gy (x, y)]²
x
Y
1 + [gx(x, y)]²+ [gy(x, y)]².
=
=
=
=
=
1 +
1 +
1 + 1/1
2/1
X
+y
x² + y²
+
y²
2.²
x² + y²
%](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2Fb3d5e6cc-70c8-4eb5-9951-03d204f22298%2F4cc01bd4-7e0e-4b59-a449-b0844243a390%2Fugo40z_processed.png&w=3840&q=75)
Transcribed Image Text:•√ √ F(x₂:
Evaluate
f(x, y, z) ds.
f(x, y, z)= √√√x² + y² + z²
S: z = √√√x² + y², (x - 1)² + y² ≤ 1
Part 1 of 6
Find the surface integral using the formula
2) ds = √ √₁²
116FX
Here, g(x, y) = Z = √x² + y². Find the partial derivatives gx(x, y) and g(x, y).
f(x, y, z) ds
gx(x, y)
gy(x, y)
X
y
f(x, y, g(x, y))√1 + [9x (x, y)]²+ [gy (x, y)]² dA.
Part 2 of 6
Substitute these partial derivatives into
1 + [9x (x, y)]²+ [gy (x, y)]²
x
Y
1 + [gx(x, y)]²+ [gy(x, y)]².
=
=
=
=
=
1 +
1 +
1 + 1/1
2/1
X
+y
x² + y²
+
y²
2.²
x² + y²
%
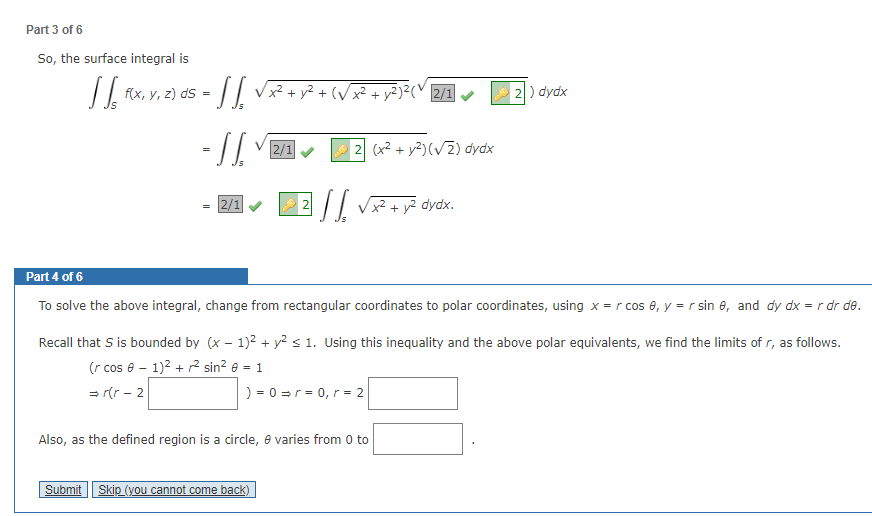
Transcribed Image Text:Part 3 of 6
So, the surface integral is
JJ, FX
s = √√√ √ x² + y² + (√x² + y² 3² (1
-SS.
-√2/1✔
f(x, y, z) ds
=
= 2/1
2
Submit Skip (you cannot come back)
2)²(2/1
Also, as the defined region is a circle, e varies from 0 to
(x² + y²)(√2) dydx
√ √ √ √ x² + y
y² dydx.
Part 4 of 6
To solve the above integral, change from rectangular coordinates to polar coordinates, using x = r cos 0, y = r sin 8, and dy dx = r dr de.
Recall that S is bounded by (x - 1)² + y² ≤ 1. Using this inequality and the above polar equivalents, we find the limits of r, as follows.
(r cos 0 - 1)² + ² sin² 0 = 1
⇒r(r-2
) = 0 = r = 0, r = 2
2) dydx
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
Need the highlighted answers in the picture below

Transcribed Image Text:Part 3 of 6
So, the surface integral is
JL. Rx
Part 4 of 6
f(x, y, z) ds =
= [[.
-=[[
Part 5 of 6
= 2/1
Il FX,
√√√x² + y² + (√√2².
To solve the above integral, change from rectangular coordinates to polar coordinates, using x = r cos 0, y = r sin 8, and dy dx = r dr de.
Recall that S is bounded by (x - 1)² + y² s 1. Using this inequality and the above polar equivalents, we find the limits of r, as follows.
(r cos 81)² + ² sin² 0 = 1
⇒r(r - 2 cos (8)
f(x, y, z) ds = 2
2/1
=
Also, as the defined region is a circle, 6 varies from 0 to Cos (0)
Substituting the above into the integral, we have
8
Cos 0
²² ²0
=
=
+26* [12²112
165 65 10
1SS. √x² + y² dydx.
cos
= 215 / 12 (
16
12 cos 8
2 (²+2)(√√2) dydx
1)=0=r=0, r = 2 cos (8)
Irir drde
2)²(2/1
drde
·[32-(sin 8-sin³6)10/²2
3
el de
π/2
2) dydx
π
- sin²8)cos 8 de
Cos 0
Solution
Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,