Show that the p.d.f. of Z? is given by g1(x) = cosh(vAr), x > 0, wh cosh(z) = }(e² + e-=) is known as the hyperbolic cosine function.
Show that the p.d.f. of Z? is given by g1(x) = cosh(vAr), x > 0, wh cosh(z) = }(e² + e-=) is known as the hyperbolic cosine function.
A First Course in Probability (10th Edition)
10th Edition
ISBN:9780134753119
Author:Sheldon Ross
Publisher:Sheldon Ross
Chapter1: Combinatorial Analysis
Section: Chapter Questions
Problem 1.1P: a. How many different 7-place license plates are possible if the first 2 places are for letters and...
Related questions
Question
DON'T COPY CHEGG GIVE NEW ANSWER OR I WILL GIVE YOU A DISKLIKE
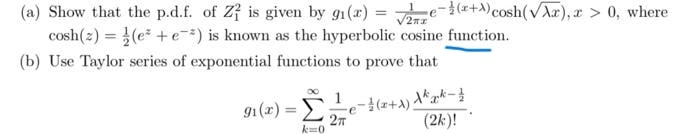
Transcribed Image Text:(a) Show that the p.d.f. of Z is given by g1(x) = e-(+)cosh(VAx), r > 0, where
cosh(2) = (e +e) is known as the hyperbolic cosine function.
(b) Use Taylor series of exponential functions to prove that
1
91(x) =
%3D
(2k)!
k=0
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 4 images

Recommended textbooks for you

A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON


A First Course in Probability (10th Edition)
Probability
ISBN:
9780134753119
Author:
Sheldon Ross
Publisher:
PEARSON
