Homework Help is Here – Start Your Trial Now!
Math
Algebra
Solve the polynomial inequality and graph the solution set on a real number line. Express the solution set in interval notation. (x-6)(x+ 4)s0 Solve the inequality. What is the solution set? Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The solution set is (Simplity your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed Use integers or fractions for any numbers in the expression.) O B. The solution set is the empty set. Which number line below shows the graph of the solution set? O B. -8 O A. -8 -7 6 7 6 5 -2-1 -3 -7 -6 -5 5 1 -3 -2 -1 -5-4 OD -8 O C. 6 7 8 5 1 -1 -3 -4 -2 -5 -6 -7 7 6 -3 2 10 12 3 -5 -6 -8 7 Click to select your answer ary ere to search W hp T PACK AR D f3 fs f6 10 + 12 ins prt sc DII delete home $ & 7 3 5 6 8 num lock backspace R T U P ho F K L enter C B pause T shift alt ctrl O I

Solve the polynomial inequality and graph the solution set on a real number line. Express the solution set in interval notation. (x-6)(x+ 4)s0 Solve the inequality. What is the solution set? Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The solution set is (Simplity your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed Use integers or fractions for any numbers in the expression.) O B. The solution set is the empty set. Which number line below shows the graph of the solution set? O B. -8 O A. -8 -7 6 7 6 5 -2-1 -3 -7 -6 -5 5 1 -3 -2 -1 -5-4 OD -8 O C. 6 7 8 5 1 -1 -3 -4 -2 -5 -6 -7 7 6 -3 2 10 12 3 -5 -6 -8 7 Click to select your answer ary ere to search W hp T PACK AR D f3 fs f6 10 + 12 ins prt sc DII delete home $ & 7 3 5 6 8 num lock backspace R T U P ho F K L enter C B pause T shift alt ctrl O I

Intermediate Algebra
Intermediate Algebra
10th Edition
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Jerome E. Kaufmann, Karen L. Schwitters
Chapter7: Equations And Inequalities In Two Variables
Section7.1: Rectangular Coordinate System And Linear Equations
Problem 46PS
See similar textbooks
icon
Related questions
Question
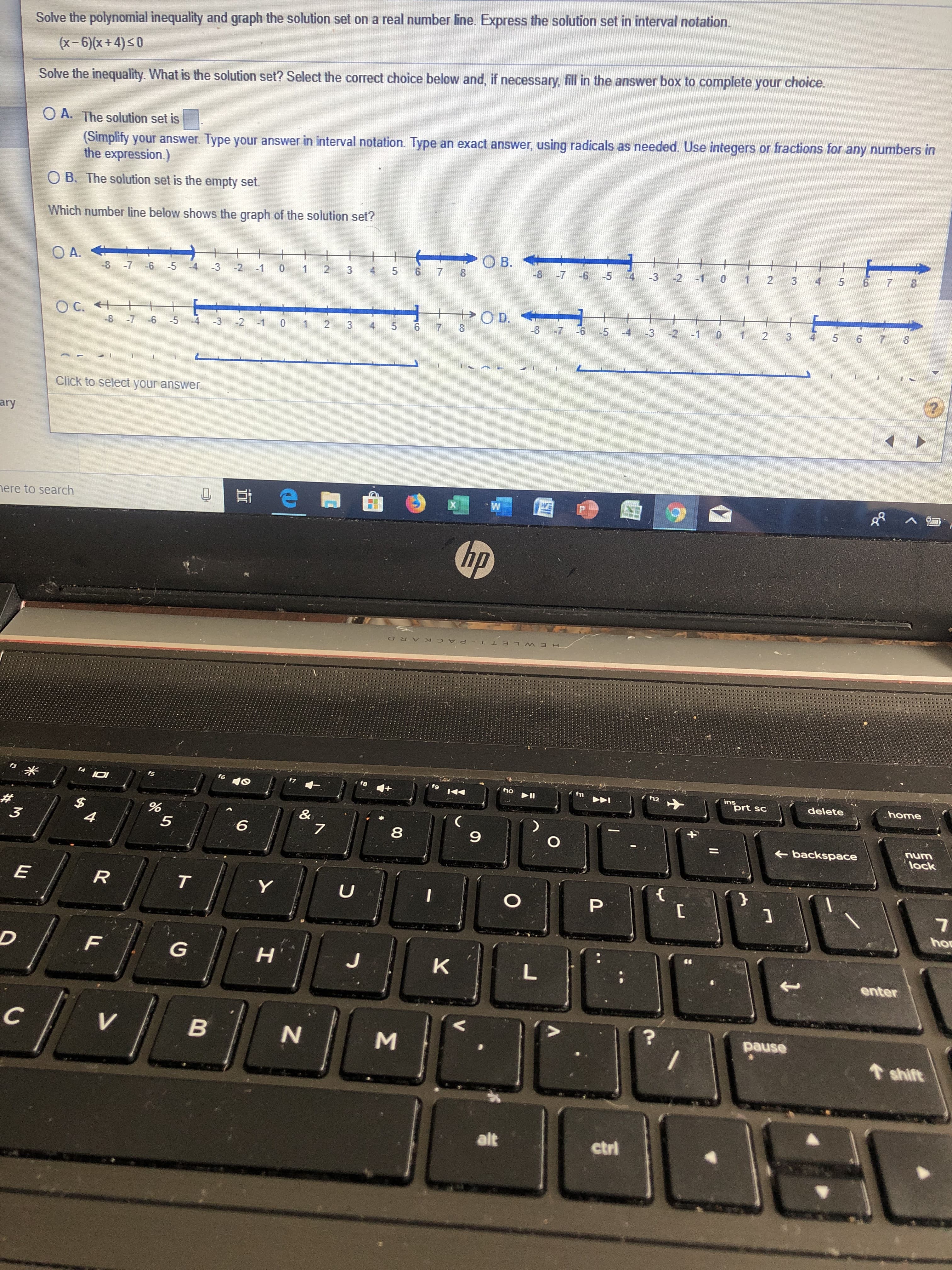
Solve the polynomial inequality and graph the solution set on a real number line. Express the solution set in interval notation. (x-6)(x+ 4)s0 Solve the inequality. What is the solution set? Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The solution set is (Simplity your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed Use integers or fractions for any numbers in the expression.) O B. The solution set is the empty set. Which number line below shows the graph of the solution set? O B. -8 O A. -8 -7 6 7 6 5 -2-1 -3 -7 -6 -5 5 1 -3 -2 -1 -5-4 OD -8 O C. 6 7 8 5 1 -1 -3 -4 -2 -5 -6 -7 7 6 -3 2 10 12 3 -5 -6 -8 7 Click to select your answer ary ere to search W hp T PACK AR D f3 fs f6 10 + 12 ins prt sc DII delete home $ & 7 3 5 6 8 num lock backspace R T U P ho F K L enter C B pause T shift alt ctrl O I
Transcribed Image Text:Solve the polynomial inequality and graph the solution set on a real number line. Express the solution set in interval notation. (x-6)(x+ 4)s0 Solve the inequality. What is the solution set? Select the correct choice below and, if necessary, fill in the answer box to complete your choice O A. The solution set is (Simplity your answer. Type your answer in interval notation. Type an exact answer, using radicals as needed Use integers or fractions for any numbers in the expression.) O B. The solution set is the empty set. Which number line below shows the graph of the solution set? O B. -8 O A. -8 -7 6 7 6 5 -2-1 -3 -7 -6 -5 5 1 -3 -2 -1 -5-4 OD -8 O C. 6 7 8 5 1 -1 -3 -4 -2 -5 -6 -7 7 6 -3 2 10 12 3 -5 -6 -8 7 Click to select your answer ary ere to search W hp T PACK AR D f3 fs f6 10 + 12 ins prt sc DII delete home $ & 7 3 5 6 8 num lock backspace R T U P ho F K L enter C B pause T shift alt ctrl O I
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 9 steps with 8 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
Intermediate Algebra
Intermediate Algebra
Algebra
ISBN:
9781285195728
Author:
Jerome E. Kaufmann, Karen L. Schwitters
Publisher:
Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897…
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition…
Holt Mcdougal Larson Pre-algebra: Student Edition…
Algebra
ISBN:
9780547587776
Author:
HOLT MCDOUGAL
Publisher:
HOLT MCDOUGAL
Elementary Algebra
Elementary Algebra
Algebra
ISBN:
9780998625713
Author:
Lynn Marecek, MaryAnne Anthony-Smith
Publisher:
OpenStax - Rice University
Intermediate Algebra
Intermediate Algebra
Algebra
ISBN:
9780998625720
Author:
Lynn Marecek
Publisher:
OpenStax College
College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS