Step 4 of 6 Calculate the energy for an electron in a 0.43-nm box using the formula from Step 3. E = 490.26 X 840 kJ-mol-1 Step 5 of 6 Calculate the exact energy for an electron in the first excited state in a 0.43-nm box. Recall that for a particle in a one-dimensional box we can write En = Eexact=49197 x KJ-mol-1 Submit n²h² we can therefore calculate an exact solution. 8mL 2'
Step 4 of 6 Calculate the energy for an electron in a 0.43-nm box using the formula from Step 3. E = 490.26 X 840 kJ-mol-1 Step 5 of 6 Calculate the exact energy for an electron in the first excited state in a 0.43-nm box. Recall that for a particle in a one-dimensional box we can write En = Eexact=49197 x KJ-mol-1 Submit n²h² we can therefore calculate an exact solution. 8mL 2'
Related questions
Question
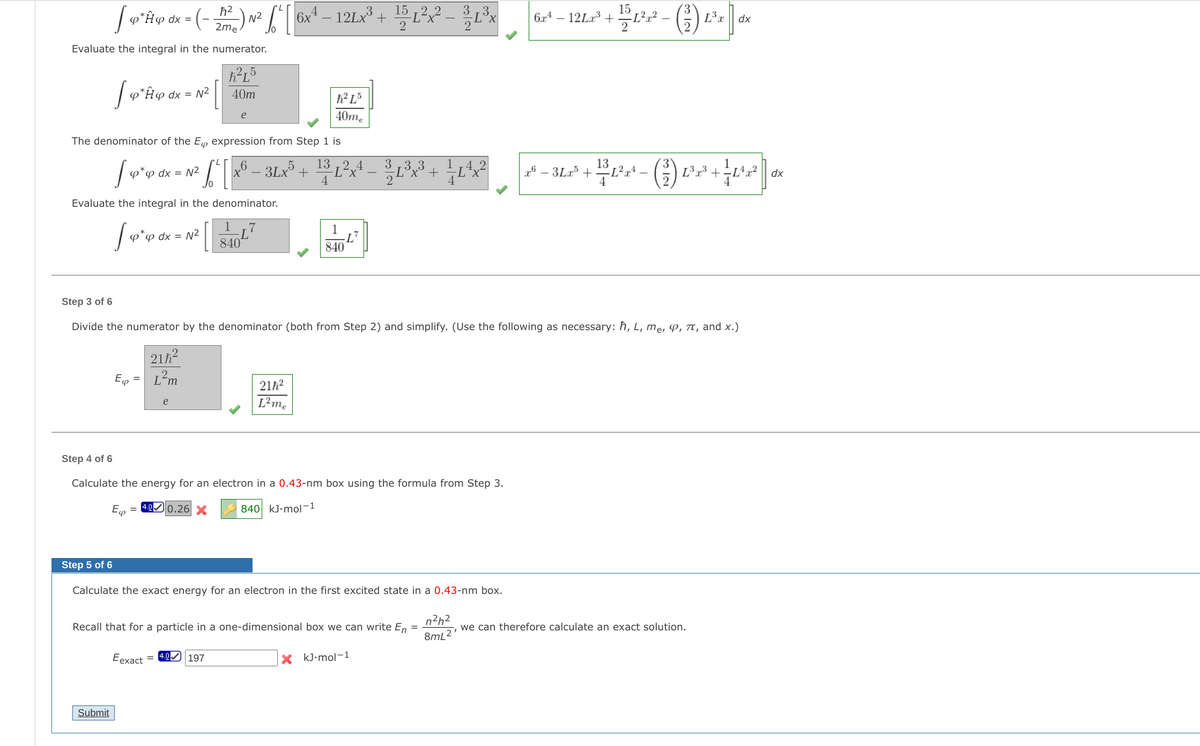
Transcribed Image Text:15
6x4 – 12Lx³ + 15 L²x? -
3,3
(-
L²r?
L3x
6r4 -
N2
2me
12La3
dx =
dx
2
2
2
Evaluate the integral in the numerator.
p*H@ dx = N²
40m
h² L³
e
40me
The denominator of the E expression from Step 1 is
6 _ 3Lx +
13 ,2 4
-L²x
4
Lx³ +
F8-3Lz' + 12rt - (%) Lz3 + +L교2
p dx = N²
dx
Evaluate the integral in the denominator.
1
1
φ φ αχx = N2
840
840
Step 3 of 6
Divide the numerator by the denominator (both from Step 2) and simplify. (Use the following as necessary: ħ, L, me, P, T, and x.)
21h?
E
L²m
21h?
L²me
e
Step 4 of 6
Calculate the energy for an electron in a 0.43-nm box using the formula from Step 3.
= 4.0 0.26 X
840 kJ•mol-1
φ
Step 5 of 6
Calculate the exact energy for an electron in the first excited state in a 0.43-nm box.
n2h2
Recall that for a particle in a one-dimensional box we can write En
we can therefore calculate an exact solution.
8mL2'
Eexact = 4.0 197
X kJ-mol-1
Submit
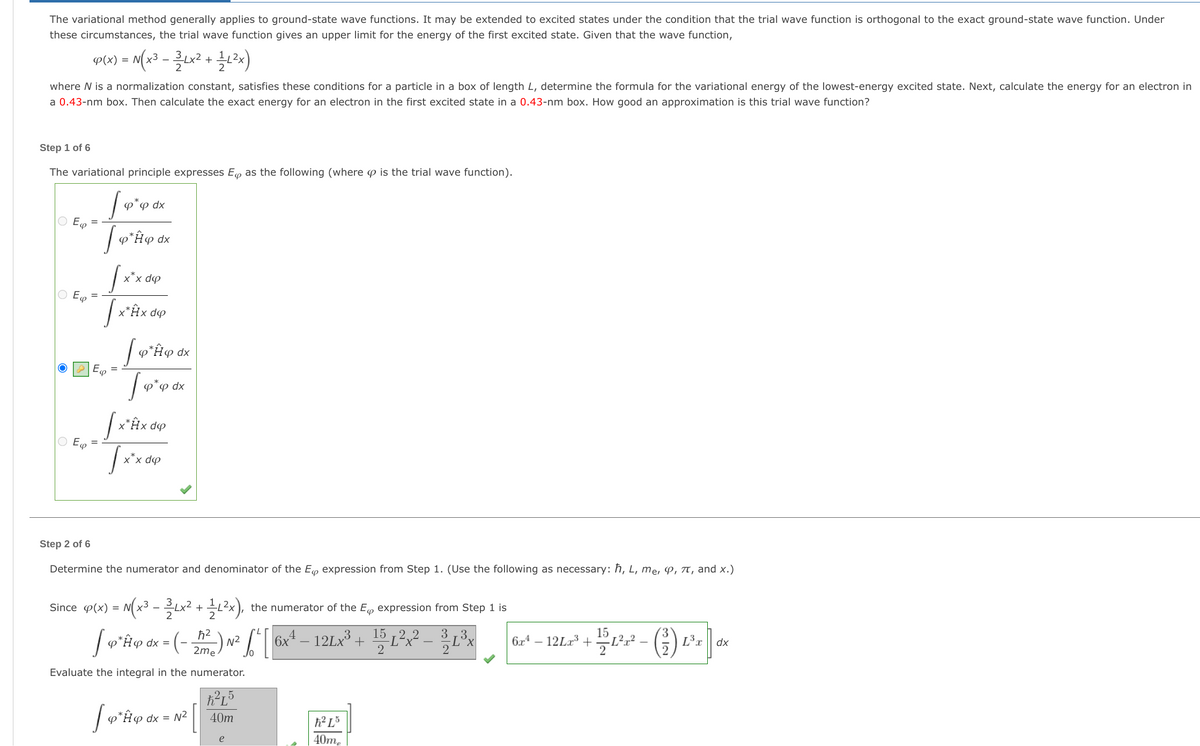
Transcribed Image Text:The variational method generally applies to ground-state wave functions. It may be extended to excited states under the condition that the trial wave function is orthogonal to the exact ground-state wave function. Under
these circumstances, the trial wave function gives an upper limit for the energy of the first excited state. Given that the wave function,
P(x) = M(x³ - Lx² + 3x)
2
where N is a normalization constant, satisfies these conditions for a particle in a box of length L, determine the formula for the variational energy of the lowest-energy excited state. Next, calculate the energy for an electron in
a 0.43-nm box. Then calculate the exact energy for an electron in the first excited state in a 0.43-nm box. How good an approximation is this trial wave function?
Step 1 of 6
The variational principle expresses Eo as the following (where p is the trial wave function).
P"P dx
O E
P
dx
x*x dp
O E =
x*Âx dp
o*¤ dx
dx
x*Hx dº
O E
x*x dp
Step 2 of 6
Determine the numerator and denominator of the E expression from Step 1. (Use the following as necessary: ħ, L, me, P, TT, and x.)
Since p(x) = N(x3 -x
+ x),
the numerator of the E, expression from Step 1 is
2 2
3
15
3.
6x – 12LX³ + 15 L
6x4 – 12La³ + Ľ²r² -
L3x
P
N2
2me
dx
2
-) -
Evaluate the integral in the numerator.
2-5
p*#@ dx = N²
40m
40m,
e
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps
