Suppose that for f, f,.. is a sequence defined as follows. fo = 5, f, = 16, fk = 7f -1- 10f-2 for every integer k 2 2 Prove that f. = 3. 2" + 2. 5" for each integer n 2 0. Proof by strong mathematical induction: Let the property P(n) be the equation f.= 3. 2" + 2 · 5". We will show that P(n) is true for every integer n 2 o. Show that P(0) and P(1) are true: Select P(0) from the choices below. O P(0) = 3- 20 + 2- 50 O f = 3- 20 + 2- 50 Ofo = 5 O P(0) = fo Select P(1) from the choices below. O P(1) = f Of = 16 O, = 3-2 +2-5 O P(1) = 3 - 21 + 2.51 P(0) and P(1) are true because 3· 20 + 2.50 = 5 and 3- 21 + 2.5 = 16. Show that for every integer k2 1, if P(i) is true for each integer i from 0 through k, then P(k + 1) is true: Let k be any integer with k 2 1, and suppose that for every integer i with o sisk, f,= This is the -Select-- We must show that f 1= Now, by definition of fo, f, f2., fk +1 = Apply the inductive hypothesis to f, and f , and complete the proof as a free response. (Submit a file with a maximum size of 1 MB.) Choose File No file chosen
Suppose that for f, f,.. is a sequence defined as follows. fo = 5, f, = 16, fk = 7f -1- 10f-2 for every integer k 2 2 Prove that f. = 3. 2" + 2. 5" for each integer n 2 0. Proof by strong mathematical induction: Let the property P(n) be the equation f.= 3. 2" + 2 · 5". We will show that P(n) is true for every integer n 2 o. Show that P(0) and P(1) are true: Select P(0) from the choices below. O P(0) = 3- 20 + 2- 50 O f = 3- 20 + 2- 50 Ofo = 5 O P(0) = fo Select P(1) from the choices below. O P(1) = f Of = 16 O, = 3-2 +2-5 O P(1) = 3 - 21 + 2.51 P(0) and P(1) are true because 3· 20 + 2.50 = 5 and 3- 21 + 2.5 = 16. Show that for every integer k2 1, if P(i) is true for each integer i from 0 through k, then P(k + 1) is true: Let k be any integer with k 2 1, and suppose that for every integer i with o sisk, f,= This is the -Select-- We must show that f 1= Now, by definition of fo, f, f2., fk +1 = Apply the inductive hypothesis to f, and f , and complete the proof as a free response. (Submit a file with a maximum size of 1 MB.) Choose File No file chosen
Chapter9: Sequences, Probability And Counting Theory
Section9.1: Sequences And Their Notations
Problem 62SE: Follow these steps to evaluate a finite sequence defined by an explicit formula. Using a Tl-84, do...
Related questions
Question
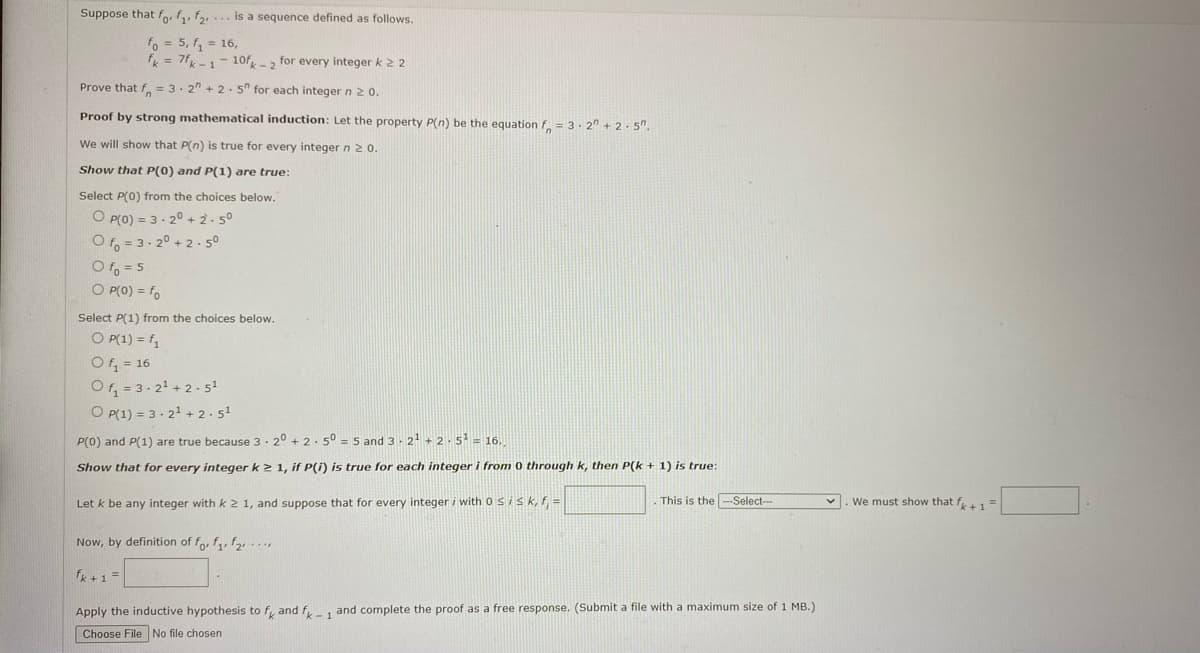
Transcribed Image Text:Suppose that for f, f,... is a sequence defined as follows.
fo = 5, f, = 16,
fk = 7f-1-10f- 2 for every integer k 2 2
Prove that f. = 3. 2" + 2. 5" for each integer n 2 0.
Proof by strong mathematical induction: Let the property P(n) be the equation f.= 3. 2" + 2 · 5".
We will show that P(n) is true for every integer n 2 o.
Show that P(0) and P(1) are true:
Select P(0) from the choices below.
O P(0) = 3- 20 + 2- 50
O f = 3-20 + 2- 50
O fo = 5
O P(0) = fo
Select P(1) from the choices below.
O P(1) = f,
Of, = 16
O = 3-2 +2.5
O P(1) = 3 - 21 + 2 . 51
P(0) and P(1) are true because 3· 20 + 2. 50 = 5 and 3- 21 + 2.5 = 16.
Show that for every integer k2 1, if P(i) is true for each integer i from 0 through k, then P(k + 1) is true:
Let k be any integer with k 2 1, and suppose that for every integer i with 0 sisk, f=
This is the -Select--
We must show that f1=
Now, by definition of fo, f, f2, -..,
fk +1 =
Apply the inductive hypothesis to f, and f- and complete the proof as a free response. (Submit a file with a maximum size of 1 MB.)
Choose File No file chosen
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 3 steps with 2 images

Recommended textbooks for you


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning