College Physics
11th Edition
ISBN: 9781305952300
Author: Raymond A. Serway, Chris Vuille
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Related questions
Topic Video
Question
thumb_up100%
![On this page, we will explore the motion of two particles in the x-y plane. The detailed analysis below will guide you through calculating various important physical quantities for the system.
**Problem Statement:**
Two particles are moving in the x-y plane.
- Particle #1 has a mass \( m_1 = 6.40 \, \text{kg} \) and is located (at any given time) by the position vector \( \vec{r}_1(t) = [0.300 \, \text{m} + (2.00 \, \text{m/s}^3)t^3]\hat{i} + 0.200 \, \text{m}\hat{j} \).
- Particle #2 has a mass \( m_2 = 9.00 \, \text{kg} \) and is located (similarly, at any given time) by the position vector \( \vec{r}_2(t) = 0.100 \, \text{m}\hat{i} + [0.300 \, \text{m} + (0.500 \, \text{m/s})t + (1.50 \, \text{m/s}^2)t^2]\hat{j} \).
Determine the following at the time \(t = 1.00 \, s\). (Express your answers in vector form.)
### Part (a) Location of the center of mass
\[ \vec{r}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{m} \]
### Part (b) Velocity of the center of mass
\[ \vec{V}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{m/s} \]
### Part (c) Acceleration of the center of mass
\[ \vec{a}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{m/s}^2 \]
### Part (d) Momentum of the center of mass
\[ \vec{P}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{kg} \cdot \text{m/s](https://content.bartleby.com/qna-images/question/d0afef86-41bd-49f7-9deb-bb70dd2f5172/352854fe-bb2f-4b2f-bda4-7a0ace8fa194/0y0jykg.png)
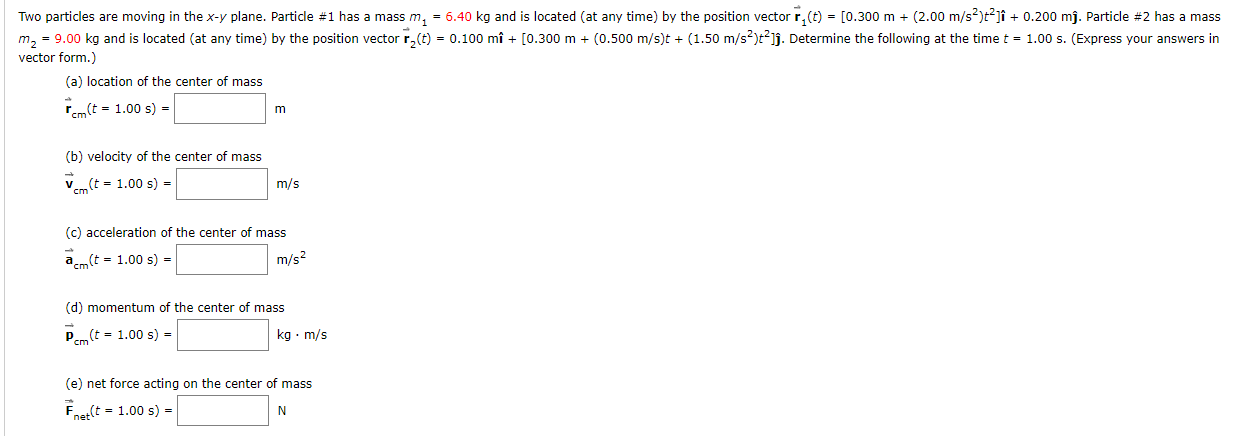
Transcribed Image Text:On this page, we will explore the motion of two particles in the x-y plane. The detailed analysis below will guide you through calculating various important physical quantities for the system.
**Problem Statement:**
Two particles are moving in the x-y plane.
- Particle #1 has a mass \( m_1 = 6.40 \, \text{kg} \) and is located (at any given time) by the position vector \( \vec{r}_1(t) = [0.300 \, \text{m} + (2.00 \, \text{m/s}^3)t^3]\hat{i} + 0.200 \, \text{m}\hat{j} \).
- Particle #2 has a mass \( m_2 = 9.00 \, \text{kg} \) and is located (similarly, at any given time) by the position vector \( \vec{r}_2(t) = 0.100 \, \text{m}\hat{i} + [0.300 \, \text{m} + (0.500 \, \text{m/s})t + (1.50 \, \text{m/s}^2)t^2]\hat{j} \).
Determine the following at the time \(t = 1.00 \, s\). (Express your answers in vector form.)
### Part (a) Location of the center of mass
\[ \vec{r}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{m} \]
### Part (b) Velocity of the center of mass
\[ \vec{V}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{m/s} \]
### Part (c) Acceleration of the center of mass
\[ \vec{a}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{m/s}^2 \]
### Part (d) Momentum of the center of mass
\[ \vec{P}_{cm}(t = 1.00 \, s) = \underline{\hspace{2cm}} \, \text{kg} \cdot \text{m/s
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 5 steps with 4 images
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Problem 2: An object of mass M is hanging from a spring (with I_o =0 and a spring constant k). There is a constant force from the wind, F_wind, blowing to the right, so the mass is initially at rest, but hanging at an angle Theta from the vertical because of the presence of the wind. Suddenly, spring breaks, and the mass drops under the influence of F_wind (note F_air and F_wind are the same constant vector!) and its weight. If the object (in equilibrium before the spring breaks) is a height H above the ground, how far laterally (in the direction of the wind) does the object hit the ground, L (given theta, k, M, g, H)?arrow_forwardAn unfortunate astronaut loses his grip during a spacewalk and finds himself floating away from the space station, carrying only a rope and a bag of tools. First he tries to throw a rope to his fellow astronaut, but the rope is too short. In a last ditch effort, the astronaut throws his bag of tools in the direction of his motion, away from the space station. The astronaut has a mass of ma = 102 kg and the bag of tools has a mass of mp = 19.0 kg. If the astronaut is moving away from the space station at Vj = 2.10 m/s initially, what is the minimum final speed vp.f of the bag of tools with respect to the space station that will keep the astronaut from drifting away forever? Ub.f = m/sarrow_forward, are: Three point particles are fixed in position in an xy plane. Two of them, particle A of mass 5 g and particle B of mass 11 g, are shown in the figure with a separation of dAB = 0.519 m at angle O = 30°. Particle C, with mass 9 g, is not shown. The net gravitational force acting on particle A due to particles B and Cis 2.71 x 1014 N at an angle of -163.8°. from the positive x axis. What are (a) the x coordinate and (b) the y coordinate of particle C? В dAB Aarrow_forward
- The proton is traveling at a constant speed of 5.5 × 105 m/s, and the radius of the kissing circle is 0.02 m. The mass of a proton is 1.7 × 10-27 kg. When the proton is at location A, what are the magnitude and direction (d|p→|/dt)(p^) of the parallel component of dp→/dt?arrow_forwardA package of mass 7 kg sits at the equator of an airless asteroid of mass 4.0 1020 kg and radius 5.9 105 m. We want to launch the package in such a way that it will never come back, and when it is very far from the asteroid it will be traveling with speed 188 m/s. We have a large and powerful spring whose stiffness is 2.1 105 N/m. How much must we compress the spring?arrow_forwardThree point particles are fixed in position in an xy plane. Two of them, particle A of mass 5 g and particle B of mass 11 g, are shown in the figure with a separation of dAB = 0.579 m at angle = 30°. Particle C, with mass 8 g, is not shown. The net gravitational force acting on particle A due to particles B and C is 2.02 x 10-¹4 N at an angle of -163.8��. from the positive x axis. What are (a) the x coordinate and (b) the y coordinate of particle C? B dAB 0 Aarrow_forward
- At the instant of the figure, a 1.00 kg particle P has a position vector 7 of magnitude 5.40 m and angle 01 = 41.0° and a velocity vector v of magnitude 4.50 m/s and angle 62 = 32.0°. Force F ,of magnitude 6.20 N and angle 03 = 32.0° acts on P. All three vectors lie in the xy plane. About the origin, what are the magnitude of (a) the angular momentum of the particle and (b) the torque acting on the particle? F (a) Number i Units (b) Number i Unitsarrow_forwardk A 13.00 kg particle starts from the origin at time zero. Its velocity as a function of time is given by = 10t² + 1tj where is in meters per second and t is in seconds. (Use the following as necessary: t.) V (a) Find its position as a function of time. ŕ= esc 10/³1 + ²/2 2²; 3 (b) Describe its motion qualitatively. The particle starts from rest at the origin, starts moving in the y direction, and gains speed faster and faster while turning to move more and more nearly parallel to the x axis. Score: 0.06 out of 0.06 Comment: (c) Find its acceleration as a function of time. a = 20ti + lj m/s² (d) Find the net force exerted on the particle as a function of time. F= T= (e) Find the net torque about the origin exerted on the particle as a function of time. N m X X (f) Find the angular momentum of the particle as a function of time. Ľ Need Help? Read It F1 N x (g) Find the kinetic energy of the particle as a function of time. K= x kg m²/s X (h) Find the power injected into the particle as a…arrow_forwardIn a train crash, a train of mass 1.85 x 104 kg collides with a stationary train of mass 2.20 x 104 kg at a speed of u = 20.0 ms-1. Filling the crash, they connect and move at the same speed. There is no friction. The train driver blows a whistle which is open at one end and closed at the other. It has a length of 0.480m . The speed of sound in air is 343 ms-1. 1. Draw a diagram of the standing wave pattern of the air pressure in the whistle for its fundamental resonant frequency. Label the open and closed ends of the whistle. 2. calculate the frequency of the sound made by the whistles fundamental resonance.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press 
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics
Physics
ISBN:9781305952300
Author:Raymond A. Serway, Chris Vuille
Publisher:Cengage Learning
University Physics (14th Edition)
Physics
ISBN:9780133969290
Author:Hugh D. Young, Roger A. Freedman
Publisher:PEARSON
Introduction To Quantum Mechanics
Physics
ISBN:9781107189638
Author:Griffiths, David J., Schroeter, Darrell F.
Publisher:Cambridge University Press
Physics for Scientists and Engineers
Physics
ISBN:9781337553278
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Lecture- Tutorials for Introductory Astronomy
Physics
ISBN:9780321820464
Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina Brissenden
Publisher:Addison-Wesley
College Physics: A Strategic Approach (4th Editio...
Physics
ISBN:9780134609034
Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart Field
Publisher:PEARSON