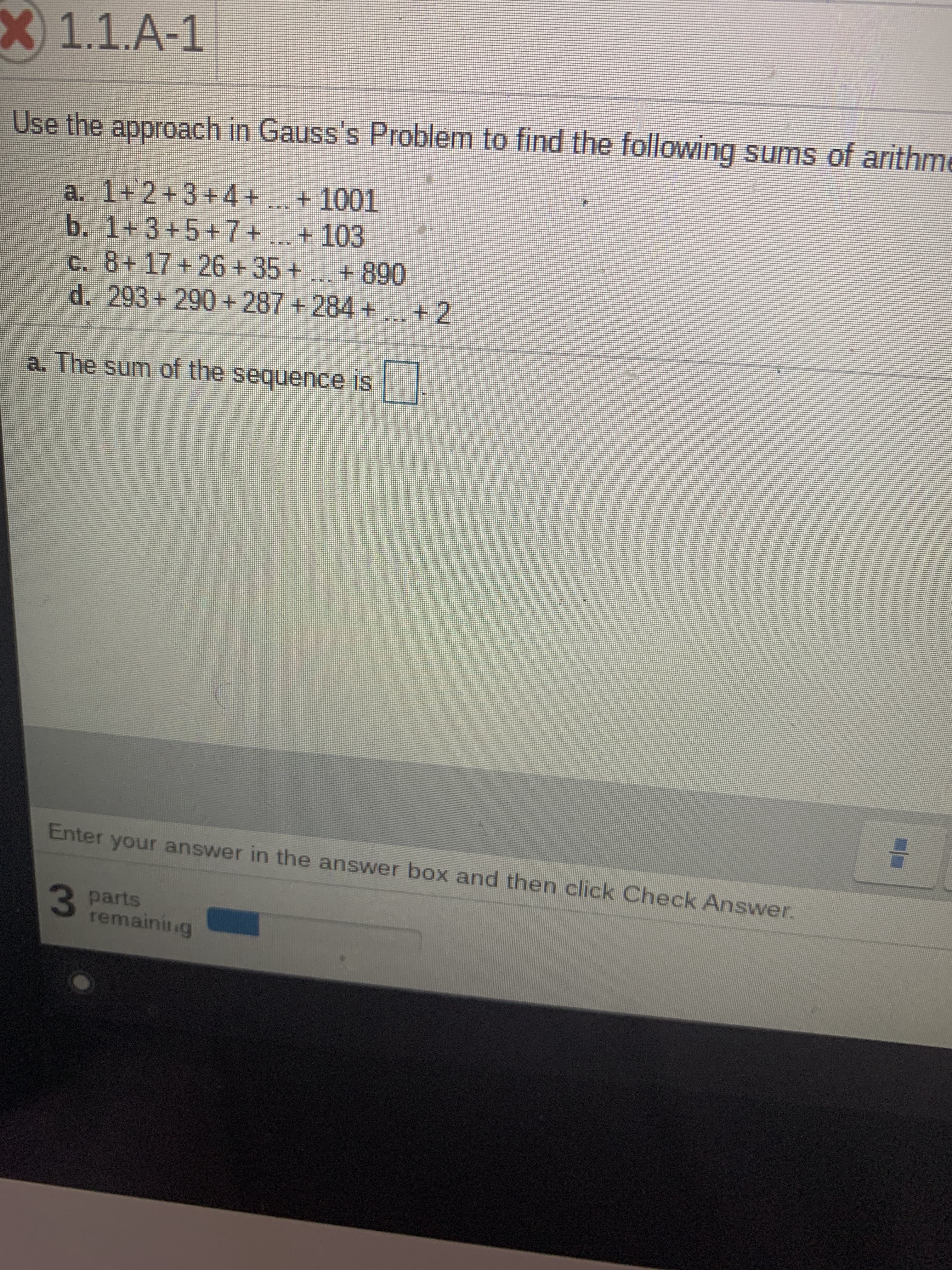
Use the approach in Gauss's Problem to find the following sums of arithmetic sequences.  A. 1+2+3+4+...+1001

Q: Given the recursive sequence tn defined below, find t4. t1 = 3 tn = tn-1 + n -2 Do not include…

A:

Q: For the sequence defined by: a1 = 1 5 An+1 = An + 4 Find: a2 az = a4 = II

A: Topic = Sequence

Q: For the sequence an = an –1 + an – 2 and a1 = 2, a2 = 3, its first term is its second term is its…

A:

Q: Use the approach in Gauss’s problem to find the following sums of arithmetic sequences (do not use…

A: To find the sum of the given arithmetic sequence using Gauss's approach.The given sequence is…

Q: Find the first four terms of the following recursively defined sequence. b-1+ 7k, for each integer k…

A:

Q: 3. Find the formula for the following sequences i. An explicit formula for 2, 6, 18, 54, 162,....…

A:

Q: For the sequence an = 5 + 3 · (n – 1), - its first term is its second term is its third term is its…

A:

Q: How many terms are there in each of the following sequences?

A:

Q: Use the approach in​ Gauss’s Problem to find the following sums of arithmetic sequences. a.…

A: According to the given information it is required to calculate the sum of the arithmetic sequences…

Q: Use the approach in Gauss's Problem to find the following sums of arithmetic sequences. a.…

A:

Q: Write out the first 10 terms of each of the following sequences (starting with ao). Then give either…

A: (a) an = 3n + 4For n = 0,

Q: Find S, for the following geometric sequences: 1, 10 100 5,-

A: Consider the following geometric sequence: 1,110,1100... First terma=1 Common…

Q: One of the formulas for finding the partial sum of an arithmetic sequence is Sn = n(a, + an). %3D O…

A:

Q: e2, e4, e6,e®,..

A: The given sequence is, e2, e4, e6, e8, … To determine whether the sequence is Arithmetic or…

Q: Find a closed form solution for the following recursive sequence: An :4an-1+5 for n > 1 with the…

A:

Q: Find the So. for each of the following sequences. 16 32 i) 20, 8, ****** 5' 25' 3-3 " 4 16 ii) 12,…

A:

Q: The non-recursively defined formula for writing an arithmetic sequence is given by: an = C+ (n -…

A:

Q: Consider the sequence {ax}, defined by a1 = 1, and ak = 2ax-1 +1 for k > 2. Compute a4.

A:

Q: 3. Match each sequence with one of the recursive definitions. Note that only the part of the…

A: A. Given sequence is 3, 15, 75, 375 Here ratio of the consecutive terms are a2a1=153=5, a3a2=7515=5,…

Q: In Problem 5, you found the closed formula for the sequence below. Use proof by induction to verify…

A:

Q: If a(1) = 2, and a(k) = 5a(k-1) for all integers k >= 2, then what is the 4th term of the sequence?

A: A sequence is a set of numbers that has a particular order or obeys a general form. Usually, the nth…

Q: For the sequence an = an –1 + an –2 and a1 = 3, a2 = 4, : 4, its first term is its second term is…

A: Given sequence is an=an-1+an-2   and a1=3, a2=4. Here,   a1 is the first term of the sequence a2 is…

Q: Find the recursive formula of the following sequence. (4, 7, 15, 24, . ... a1 = 4, a, = an-1+ 3(n +…

A:

Q: Use the approach in​ Gauss’s Problem to find the following sums of arithmetic sequences.   a. 1 + 2…

A:

Q: For the sequence an = an –1 + An – 2 and a1 3, a2 = 4, | its first term is its second term is its…

A: Given, a1 = 3 a2 = 4 an = an-1 + an-2

Q: Consider the following recursively defined sequence. tk = tx - 1+ 3k + 1, for each integer k 2 1 to…

A:

Q: Use the approach in​ Gauss’s Problem to find the following sums of arithmetic sequences.…

A:

Q: The general term for the sequence , . is: 3n n+1 3n 3+2 n+3 n+1

A: Given:     To determine: The general term of the given sequence.

Q: For the sequence defined by: 2 1 - 3 An a1 || аn +1 Find: a2 az = a4 = II

A:

Q: Refer to the following arithmetic sequence: 2, 10, 18 , 26, 34, 42, .... What is a recursive formula…

A:

Q: For the sequence defined by: a1 = 3 1 An +1 = an + 4 - Find: a2 = az = аз a4 = Submit Question

A:

Q: Use the approach in Gauss's Problem to find the following sums of arithmetic sequences.…

A:

Q: For the sequence an = An –1 + an – 2 and a1 1, a2 = 2, its first term is its second term is its…

A:

Q: Write out the first 5 terms (starting with ao) of each of the sequences described below. Then give…

A:

Q: Start with any arithmetic sequence of the form s(n) = an + d for n=1,2, ... and fixed positive…

A:

Q: Which of the following conjectures describes the pattern of the sequence 2, 4, 8, 16, 32? * O Two is…

A: Given: 2, 4, 8, 16, 32?

Q: Is the sequence shown in the picture bounded? Why or why not? What work has to be done to show if a…

A: The given sequence is: an=1,4,7,10,.....  Given sequence is a arithmetic progression with: an…

Q: Use the approach in​ Gauss’s Problem to find the following sums of arithmetic sequences. a. 1 + 2 +…

A:

Q: Consider a sequence defined on the set of non-negative integers as follows: an = -2(-1)" for n 2 0.…

A: Since you have asked multiple question, we will solve the first question for you. If you want any…

Q: Determine the explicit formula for the following sequences. 2. Sequence: 6, -6, 6, –6, 6, ... a, = 6…

A: Solution is given below:

Q: Suppose that a sequence is defined as follows. a1 =-4, an= 3a,-1+7 n2 2 for List the first four…

A:

Q: Use the approach on Gauss's problem to find the following sums of arithmetic sequences…

A:

Q: Use the approach in​ Gauss’s Problem to find the following sums of arithmetic sequences. I need help…

A: Gauss’s approach to find the sum of arithmetic sequences is as follows. Consider the sequence…

Q: use the approach in Gauss's problem to find the following sum of arithmetic sequences.…

A: Topic = Series

Q: Use the approach in​ Gauss’s Problem to find the following sums of arithmetic sequences.   a.…

A:

Q: Find the first six terms of the piecewise sequence: S( - 2)" (– 2)" – 3 if n is even an = | 3-1 – 4…

A: n=1 , 3 , 5 are odd, so we use the second piece

Q: Let be the arithmetic sequence defined by the formula a = 11 + (n-1) × 6 Apply the concepts of the…

A: Given tn= 11 + (n-1) × 6 Compare with tn= a+ (n-1) d⇒a=11,d=6

Q: Refer to the following arithmetic sequence: 2, 10, 18, 26, 34, 42, ... What is a non-recursive…

A:

Q: Find the 15th term of the following sequence. {64, 16, 4, 1, ...} a 0.000000212 b 0.0000000543…

A: Topic :- Sequence Correct answer = d

Q: Use the approach in Gauss's Problem to find the following sums of arithmetic sequences. a. 1+2+3+4+.…

A:

Sequence and Series

A sequence is defined as a collection of things. Series is defined to sum the things one by one in the sequence.  It was invented by German mathematician Carl Friedrich Gauss.