Verify that the function f(x)= x-3x+2 satisfies the hypotheses of the Mean Value Theorem 6. on the interval-2, 2. Then find all numbers x=c that satisfy the conclusion of the Mean Value Theorem
Verify that the function f(x)= x-3x+2 satisfies the hypotheses of the Mean Value Theorem 6. on the interval-2, 2. Then find all numbers x=c that satisfy the conclusion of the Mean Value Theorem
Chapter3: Functions
Section3.3: Rates Of Change And Behavior Of Graphs
Problem 2SE: If a functionfis increasing on (a,b) and decreasing on (b,c) , then what can be said about the local...
Related questions
Question
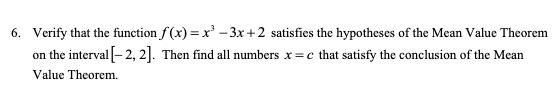
Transcribed Image Text:Verify that the function f(x)= x-3x+2 satisfies the hypotheses of the Mean Value Theorem
6.
on the interval-2, 2. Then find all numbers x=c that satisfy the conclusion of the Mean
Value Theorem
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images

Recommended textbooks for you


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning