Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter1: Fundamental Concepts Of Algebra
Section1.3: Algebraic Expressions
Problem 44E
Related questions
Question
Finding a One-Sided Limit In Exercises find the one-sided limit (if it exists).
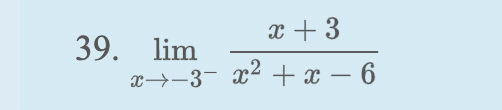
Transcribed Image Text:x + 3
39.
lim
x→-3- x² +x – 6
Expert Solution
Step 1
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning
Expert Answers to Latest Homework Questions
Q: Briefly describe the importance of communication
Q: Give the definition of Corporate Communication
Q: Janice and Jonathon operate a self-service car wash facility in partnership sharing profits equally.…
Q: Consider the series RLC circuit, represented in the Figure below:
Figure - Series RLC circuit.
The…
Q: 1-7) An elevator is traveling upwards with constant acceleration aɛ = 1 m/s². A stone is dropped…
Q: A block diagram of a control system is a representation of the functions performed by each component…
Q: You come up with a CNN classifier. For each layer, calculate the number of weights, number of biases…
Q: Discuss critically how brands can use social media to develop greater media value.
Q: You want to cluster 7 points into 3 clusters using the k-Means Clusteringalgorithm. Suppose after…
Q: It was once predicted that the internet would replace large central stores and that within ten years…
Q: Sean Zane is a Carpenter who operates a shop in Kingston, Jamaica. The shop generates income of…
Q: Compare the effectiveness of different methods of online advertising, including programmatic display…
Q: Explain the main advantages that a company selling consumer products could derive through the…
Q: Albert Camus considered the question of whether to commit suicide to be the fundamental problem in…
Q: QUESTION 2
2.1. Find the value of -3x²+ 8x-15 if x = -2.
2.2. (a) Add the following polynomials:…
Q: An object is placed 65 cm from a glass lens (n = 1.52)
with one concave surface of radius 23.0 cm…
Q: are Common to all Substance.
of
②State the three assumptions
Kinetic theory of matter!
⑥Distinguish…
Q: Assume that cost curves have the standard U-shape. Suppose average total cost (ATC) is at its…
Q: This time we have a crate of mass 29.9 kg on an inclined surface, with a coefficient of kinetic…
Q: 9:38....
89
Assignment 3_ECE 161.pdf
Assignment 3 (CLO 3)
ECE-161 Digital Logic Design
Deadline:…
Q: You have entered into a forward contract with the following parameters:
Bond:
5 year, zero coupon…