What is a Limit?
When it comes to calculus, limits are considered to be a very important topic of discussion. The main importance of limit lies in expressing the value of a function as it gets closer to a certain value. Also, limits can help you to understand other topics, such as continuity and differentiability better. In a broader sense, every calculus notion is a limit. Other branches of calculus have also been derived from limits.

How is Limit Interpreted?
For example, let us take the function given below-
In the above function, f(x) has been defined at all of the points. The only exception is when x = a, because the value of the function at that point takes the form 0/0. In mathematical terms, this is an indeterminate form. However, we may still need to know the value of the function when x is close to a, but not exactly at a. This is a limiting behavior, and this behavior in the neighborhood is known as the limit function, provided is very small.
This states that x is very close to a, but not a. In such a case, the notation of the limit is-
If we consider , it means that as x approaches point a, then the function tends to have the value . In other words, it can be said that if x is so chosen that it belongs in the neighborhood, then the difference of and can be reduced as much as we want.
In math's, we write
such that
Here, ε and δ are positive numbers having a very small value, and ε is dependent on δ.
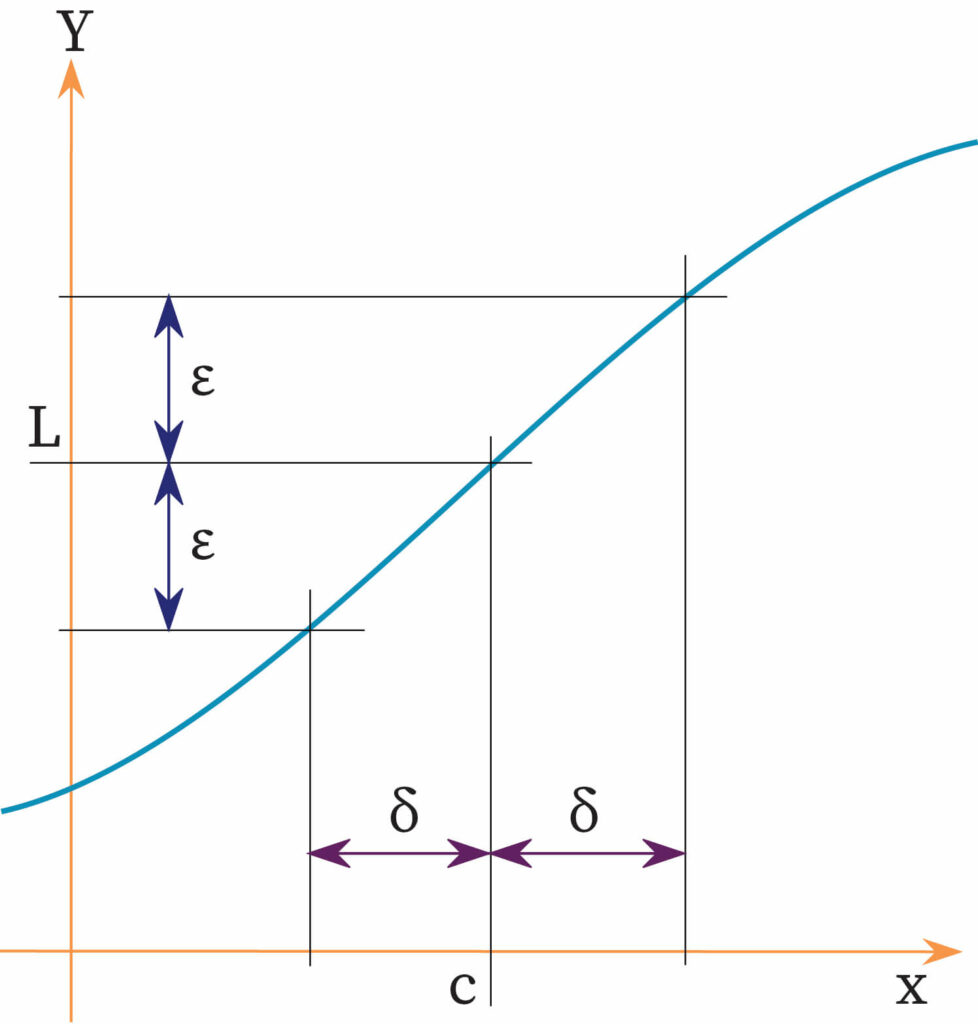
By now, we can understand the conditions in which the limit of at , would exist.
It will only exist if and only if the following conditions are satisfied-
- In the neighborhood of , is a well-defined function.
- The function shows a unique behavior when it is present in the neighborhood.
Is Limit a Finite Number?
In simple terms, a limit is not restricted to be a finite number only. It is completely possible to get an infinite limit for as x approaches a.
If , then it means that is in the neighborhood, and can possibly be equal to a quite large positive value.
For instance, equals to ∞ (infinity) in the neighborhood of .
How can we Interpret the Limit of a Function Through Graphs?
In any case, we can ignore the fact of whether or not the given function is defined at the required point. However, we have to prioritize the value that the function takes at a certain point. With graphs, it is easy to determine when-
- The function is defined at the particular point
- When it is not defined at the point, or
- When the function is defined at the point, but the value is different from the limit.
What are Left and Right Limits?
If we consider a function as , and the point of consideration as , then-
- Left limit equals the left tendency of the function at .
- Right limit equals the right tendency of the function at .
The left limit and right limit are usually denoted by or and or respectively.
By definition,
Here, h is considered to have a small positive value.
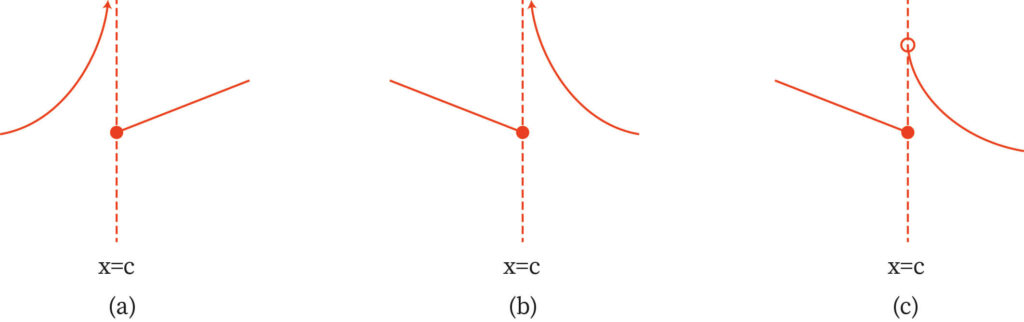
Hence, we see that for the limit of to exist at , the value of must be equal to the value of , or the left limit should be equal to the right limit, given that the limits are finite in value. If not, then (+ ∞) or (- ∞) should be the value of both the left limit and right limit.
Corollary
It is not necessary that the function is to be defined at , for the limit at , to exist. However, can exist even with or without the existence of the limit. If the limit does exist, then the value may not be the same as .
What are One-Sided Limits?
Previously, we have seen that the left limit of the function equals the right limit. However, in some cases, we see that that the value of the function at the right-hand side exists, but no left neighbourhood exists as the function approaches the given point.
Similarly, it is also possible that the left-hand limit exists, but the other neighborhood does not exist in the same domain for the same point. Thus, even if the function approaches the given point, limits can be defined at one side only. These are known as one-sided limits.
When is a Function Said to be Indeterminate?
In some special cases, the functional values take the following forms-
In all such cases, the functions are termed to have indeterminate forms.
The cases and are often considered to be the standard indeterminate form, and in such cases, L'Hospital's rule is applicable. With L'Hospital's rule, the numerator and the denominator are both differentiated until the indeterminate form goes away.
It is also important that we do not have the option to manipulate the function as we may seem fit. For example, for a function is not equal to.
This is because it could have only been written if x is not equal to a, or if, is not equal to zero. When x equals a, such restrictions prevent us from manipulating the function. This is because there is no break at the function when x equals a. Therefore, we can only interpret that function has a finite value at a point that is infinitesimally close to a.
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science in Mathematics
- Master of Science in Mathematics
Want more help with your calculus homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Limits Homework Questions from Fellow Students
Browse our recently answered Limits homework questions.