Algebra & Trigonometry with Analytic Geometry
13th Edition
ISBN:9781133382119
Author:Swokowski
Publisher:Swokowski
Chapter1: Fundamental Concepts Of Algebra
Section1.2: Exponents And Radicals
Problem 39E
Related questions
Concept explainers
Rate of Change
The relation between two quantities which displays how much greater one quantity is than another is called ratio.
Slope
The change in the vertical distances is known as the rise and the change in the horizontal distances is known as the run. So, the rise divided by run is nothing but a slope value. It is calculated with simple algebraic equations as:
Question
Each limit represents a derivative f '(a). Find f (x) and a.
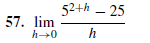
Transcribed Image Text:52+h – 25
57. lim
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Recommended textbooks for you

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage