What is the Ratio (rate)?

The relation between two quantities which displays how much greater one quantity is than another is called ratio.

Ratios (rates) are related to everyday life. For example, the speed of a bike is a rate. The amount of simple interest paid each month is a rate.

Example:

There are 30 students in the classroom, of which 12 are boys and 18 are girls.

The ratio of boys to girls is $\frac{12}{18}= \frac{2}{3}$. That is 2:3.

The ratio of girls to boys is $\frac{18}{12}= \frac{3}{2}$. That is 3:2

The ratio of girls to all students is $\frac{18}{30}= \frac{3}{5}$. That is 3:5.

The ratio of boys to all students is $\frac{12}{30}= \frac{2}{5}$. That is 2:5.

What is the Rate of Change?

The rate of change is the speed at which a variable changes from one place to another place over a specific period of time. The rate of change is usually expressed as a relation between the change in one quantity corresponding to a change in another. Graphically, the rate of change is determined by the slope of a line. The rate of change is often represented by the Greek letter delta.

The understanding of the rate of change from one quantity to another is of major importance to the study of both integral and differential calculus.

The rate of change is not only used in the mathematics branch, it is also used in physics, chemistry, economics, and finance branch.

Formulas for Rate of Change

Rate of change is a rate that defines how the change in one variable is related to the change in other variables.

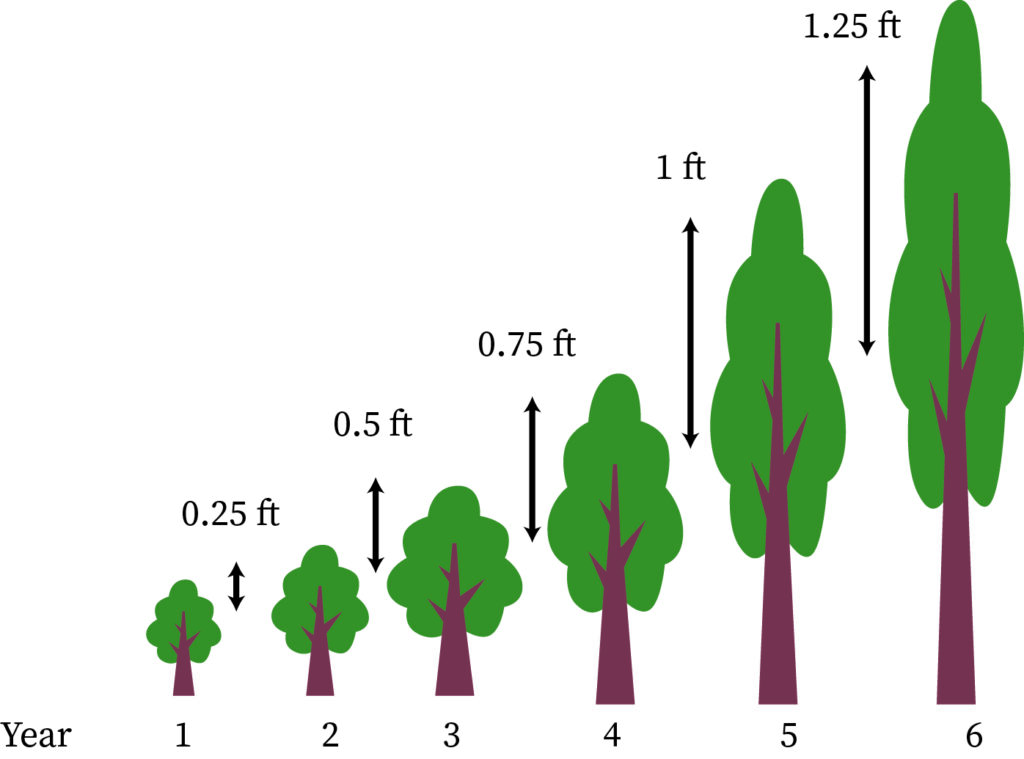
From the above figure, it is shown that how much the height of the tree increased with the increase in a year (time).

Here year (time) is the independent variable and the tree’s height is the dependent variable. The increase in height is dependent on the change in time.

If x is an independent variable and y is a dependent variable then the rate of change is

If x and y are dependent variables and s is an independent variable, and the two variables x and y change with respect to s then the rate of change of y  with respect to x  will be,

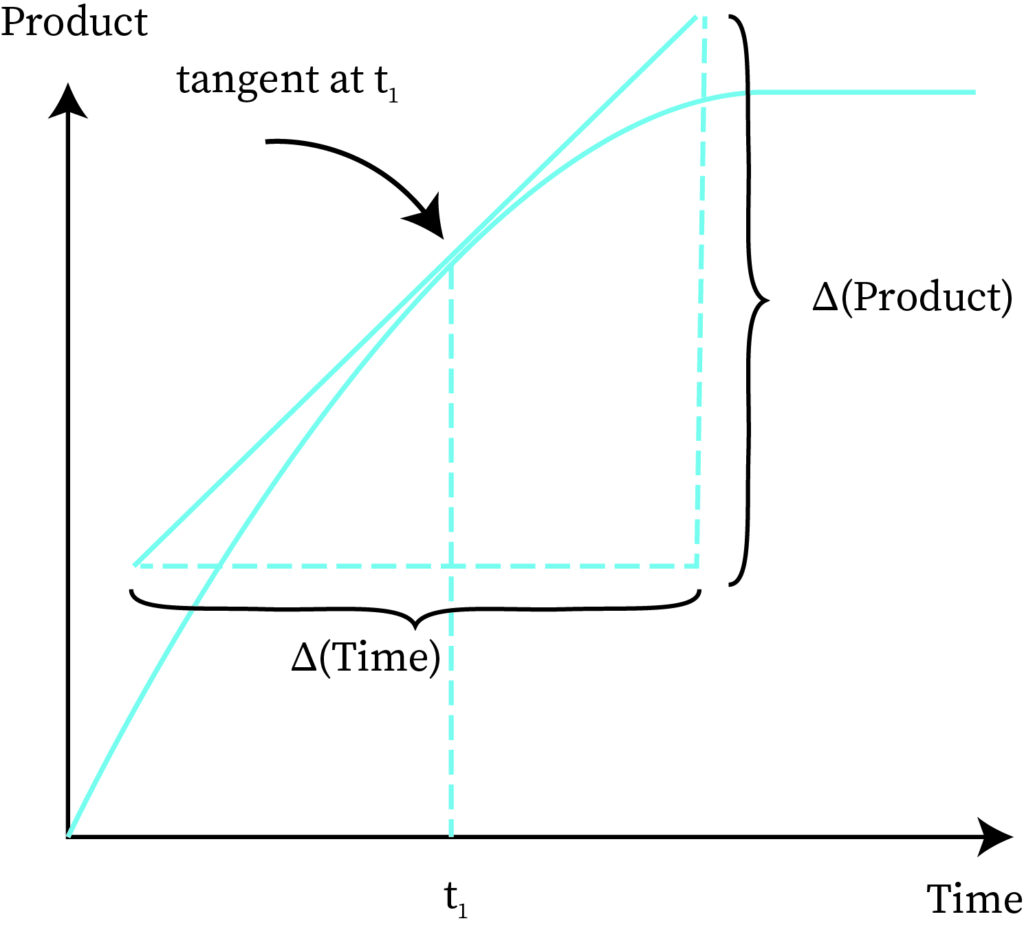
Graphically, the rate of change is represented as the slope of the curve.

From the graph, the rate of change is $\frac{y_2-y_1}{x_2-x_1}$. This is also called the slope of the line.

From the graph, the increment in x value causes an increment in the y value. So the rate of change is positive.

If the increment in x value causes a decrement in the y value, then the rate of change is negative.

If the increment in the x value causes no change in the y value, then the rate of change is zero.

Average Rate of Change

The average rate of change of a function f on the interval [a, b] is defined as $\frac{f(b)-f(a)}{b-a}$.

Example 1:

The price of petrol increased by $3.50 from 2014 to 2021. Find the average rate of change?

The price increment is $3.50.

The rate of change = $\frac{3.50}{2021-2014}=\frac{3.50}{7}=0.5$

The price of petrol increased by about $0.5 per year.

Example 2:

How is the value of y changing between the points (2, 4) and (4, 8)?

Solution:

Here, (x₁, y₁) = (2, 4) and (x₂, y₂) = (4, 8)

The rate of change = $\frac{y_2-y_1}{x_2-x_1}=\frac{8-4}{4-2}=\frac{4}{2}=2$

There is 2 units change in y value per unit change of x value.

Theoretical Example

Let x be the weight of the object and y be the length of the spring. If the weight of the object increased by Δx, let the amount of change produced in the length of the spring as Δy.

So, the rate of change is $\frac{\Delta y}{\Delta x}$.

Physics Example

A particle has a position ‘x’ at the time ‘t’, i.e., the position of the particle is x(t). This is called displacement. The rate of change of the particle’s position ‘x’ with time ‘t’ is known as the velocity ‘v’ of the particle.  That is, the rate of change of displacement is called velocity.

The rate of change of velocity ‘v’ is called the acceleration ‘a’ of the particle.

Instantaneous Rate of Change

The instantaneous rate of change is the change in the rate at a specific instant, and it is equal to the derivative value at that specific point.

For the function $f\left(x\right)=2x^2+2$, the instantaneous rate of change at $x=5$ is calculated as:

$f\left(x\right)=2x^2+2$

$f\text{'}\left(x\right)=4x$

$f\text{'}{\left(x\right)}_{x=5}=4\left(5\right)=20$

The instantaneous rate of change at $x=5$ is 20 units.

The formula for instantaneous rate of change = $f^{\prime }\left(a\right)=\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}$

Economics example

Marginal cost and revenue are used to determine the volume of production and the price per unit of a product that will get the best out of profits.

The marginal cost of production determines the variation in the entire price of a good that rises from manufacturing one supplementary unit of that good.

The marginal cost (MC) is calculated by dividing the variation (Δ) in the entire price (C) by the variation in quantity (Q).

By calculus, the marginal cost is computed by taking the first derivative of the entire price function with respect to the quantity.

Price Rate of Change

The rate of change is used to find the change in price in a particular period. This is known as the price rate of change. The price rate of change is the price of a product at time B minus the price of the same product at time A and dividing that result by the price at time A.

Price rate of change$=\frac{B-A}{A}$

For example, the rate of gold is $54 today and five days before the rate was $50, then the price rate of change is $\frac{54-50}{50}=0.08$

In five days rate is increased 8%.

Application of Rate of Change

• To find a new value of a quantity from the old value and total change.
• To find the movement of the particle, velocity (speed), and acceleration of a particle moving along a straight line.
• To calculate the upcoming population from the current population growth rate.
• To compute marginal cost and revenue in a business situation.
• The rate of change is used to find the exchange rate, inflation rate, interest rate, price-earnings ratio, rate of return, tax rate, unemployment rate, and wage rate.

Formulas

Context and Applications

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for      

• BBA
• B.COM
• M.COM