Answered: Shopping mall Farmers Home Pet store…

Shopping mall Farmers Home Pet store market Pharmacy Home 18 27 15 8 - Pet store 18 24 22 10 Shopping mall 27 24 20 32 - Farmers market 15 22 20 22 - Pharmacy 10 32 22 -

Calculus For The Life Sciences

2nd Edition

ISBN:9780321964038

Author:GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.

Publisher:GREENWELL, Raymond N., RITCHEY, Nathan P., Lial, Margaret L.

Chapter12: Probability

Section12.CR: Chapter 12 Review

Problem 64CR

See similar textbooks

Related questions

Q: Use the following information for questions 3-6. The columns indicate the number of trains running.…

A: Calculate the net benefit = total railroad profit - total lost profit for farmers for each number…

Q: Q2. Suppose you have been appointed the County Executive in charge of finance in your County. You…

A: Given Solution: The solution of the given problem is as follows:- (I) Solution:-

Q: 1 2 3 Supplies 4 5 || 1

Q: DISCRETE MATH: SCHEDULING The following table shows the activities A, B, C, D and E, involved in a…

A: (a) Activity network Start with the independent activities A and B and continue with the dependent…

Q: Use the decreasing time algorithm to create a priority list for the digraph below, then schedule the…

A: Given:

Q: A sales director who lives in city A is required to fly to regional offices in cities B, C, D, and…

A: Image is attached with detailed solution.

Q: C F -15- 6. 12- В E 14 -4- A D Apply the sorted edges algorithm to the graph above. Give your answer…

Q: Q3. Solve the following LP problem by using The Simplex Algorithm. (Keep loyal to the Simplex…

A: Problem is Max Z = 3 x1 + 5 x2 + 6 x3subject to2 x1 + x2 + x3 ≤ 4x1 + 2 x2 + x3 ≤ 4x1 + x2 + 2…

Q: Consider the following IP. The optimal tableau for this IPs linear programming relaxation is also…

A: given max z=2x1-4x2s.t.2x1+x2≤5-4x1+4x2≤5x1, x2≥0; x1 ,x2 integer use the cutting plane algorithm…

Q: An unmanned rover must be routed to visit four sites labeled A, B, C, and D on the surface of the…

A: The question is from traveling salesman problem. Here, the problem demands the shortest possible…

Q: Home You have five errands to run around town in 10 2 no particular order. You must visit the post…

A: According to question We have five errands to run around town in no particular order. You must visit…

Q: В 24 17 5. A -11 15 20 8. 8. 25 21 -12 F D 16 E

A: Consider a given figure:

Q: S Worksheet 2- Math 101 (USE A PENCIL) 1) Shown in the table below are the one-way airfares between…

A: Since you have asked multiple question, we will solve the first question for you. If you want any…

Q: PROBLEM SET (Mathematics of Graphs) 1. Nicole wants to tour Asia. She will start and end her journey…

A: 2) To find: low-cost route for the traveler First we draw Weighted graph from given data

Q: 2. CarpetPlus sells and installs floor covering for commercial buildings. Brad Sweeney, CarpetPlus…

Q: A major hotel chain is constructing a new resort hotel complex in Greenbranch Springs, WestVirginia.…

A: Given: A major hotel results in constructing new resort. This will be wooded area in which the…

Q: Solve the following linear programs (LPs) using the simplex algorithm. • For each tableau you…

Q: 3. Show the starting solution for the following problem using the three methods: 1 3 4 Supply 1 100…

Q: You are having a Christmas vacation in Europe. You want to visit these four different beautiful…

A: The time taken to visit each place from home is given as follows: Home Place A Place B Place C…

Q: Solve the following linear programs (LPs) using the simplex algorithm. • For each tableau you…

A: Given linear problem is minimize zx1, x2 =-x1-x2subject to,x1+x2 ≤4x1 ≤3 x2 ≤3x1,…

Q: The table below shows the cost of direct train travel between various cities. QUESTION A: Draw a…

A: Given:

Q: Using the Sorted Edges Algorithm find the cost of the Hamiltonian circuit for the graph below. 6, 5.…

A: write the edges with their weights as follows AC-2AD-6AB-5DC-5DB-8CB-4 Sort the edges from the…

Q: Scott and Associates, Inc., is an accounting firm that has three new clients. Project leaders will…

A: (a) The network is shown below.

Q: For the graph shown below, compute for the total weight of a Hamiltonian cycle using the…

A: Here we use edge picking algo.

Q: When using the simplex algorithm, an error was made in choosing the pivot row. Which of the…

A: If you make a mistake in choosing the pivot row in the simplex method, the solution in the next…

Q: 2. Adelina needs to do some shopping the day after Easter to buy yummy Nerds Jelly Beans. She finds…

A: First We have to find shortest route then have to find minimal spanning tree

Q: 2.2. Solve the following linear programs using the simplex method. If the problem is two…

Q: 11 4. 10 6. 2 6. 3.

Q: Applications of Weighted Graphs (Aufmann) Route Planning: Brian needs to visit the pet store, the…

A: A path that starts at any vertex of the graph and visits every vertex of the graph exactly once is…

Q: B 24 17. A -11- 15 21 20 25 21 F -12- D 16 E

A: In edge-picking algorithm we start with the edge that has the smallest weight. Then, the edge with…

Q: 1. Vincent needs to visit the pet store, the shopping mall, the local farmers market, and the…

Q: 2) Determine the minimum tree number and its weights using Prim's algorithm, starting from point C…

Q: I B 14- 13 -15- 127 11. F E Apply the sorted edges algorithm to the graph above. Give your answer as…

Q: Consider the following graph. A 2 B 1 D с How many unique (excluding reverse) Hamiltonian circuits…

A: We have given a graph having 4 vertex ABCD and is a complete graph. We have to find: 1. How many…

Q: A sales director who lives in city A is required to fly to regional offices in cities B, C, D, and…

Q: 2. Adelina needs to do some shopping the day after Easter to buy yummy Nerds Jelly Beans. She finds…

A: Let H,G,T,W represents Home, Giant Eagle, Target and Walmart.

Q: Generate the dual simplex iterations for the following problems (using TORA for convenience), and…

A: Dual Simplex Method Algorithm: Step1: Convert the problem to maximization if it is in minimization…

Q: Consider the weighted graph representing towns A to H and the roads connecting the towns marked by…

A: Given graph: a=1, b=1, c=6, d=5, e=2, f=5; and ab=1x1=1, bc=1x6=6, cd=6x5=30, de=5x2=10, ef=2x5=10,…

Q: Nicole wants to tour Asia. She will start and end her journey in Tokyo and visit Hong Kong, Bangkok,…

A: The missing weights are as follows: A = 470 B = 225 C = 520

Q: Solve the following problem using the tableau implementation of the simplex algorithm. minimize -…

A: Min Z = - 6 x1 - 4 x2 + 2 x3 subject to x1 + 2 x2 + 4 x3 ≤ 20 - 5 x2 + 5 x3…

Q: Home Hospital Mall Esplanade Pet Shop Home 2.00 km/h 4.00 km/h 3.53 km/h 6.00 km/h Hospital 2.00…

A: 1st picture

Q: Solve the following linear programs (LPs) using the simplex algorithm. • For each tableau you…

A: Optimal solution can be found by using simplex method . If int he minimum ratio , does not exist…

Q: Use the simplex algorithm to solve the following linear optimisation problem:…

A: # since the question do not mention which steps of algorithm that are presented in the course notes…

Q: In the following directed graph construct the Weight Matrix, and use Dijkstra Algorithm to evaluate…

Q: Apply traveling salesman algorithm to find a route with the least total airfare that visits each of…

A: Let S stands for San Francisco. L.A for Los Angles. D for Denver. Det for Detroit NY for New York S…

Q: A truck must deliver furniture to stores located in five different cities A, B, C, D, and E. The…

A: Optimal tour for the truck, if the travel along the diagonal.

Q: a) is your colleague correct in their assertion? if not, how would you explain to them why this…

A: A simplex table is optimum table and we get the optimal solution if the value of reduced cost of…

Q: The prices for traveling between five cities in Colorado by bus are given in the table below. Use…

A: Given- The prices for travelling between five cities in Colorado by bus are given in the table…

Q: In this exercise a graph is used to help solve a scheduling problem. Twelve faculty members in a…

A: Given:Twelve faculty members in a mathematics department serve on the following…

Q: 3. Travel Nicole wants to tour Asia. She will start and end her journey in Tokyo and visit Hong…

A: Given: table of airfares between cities. we are going to use greedy algorithm to find low-cost…

Question

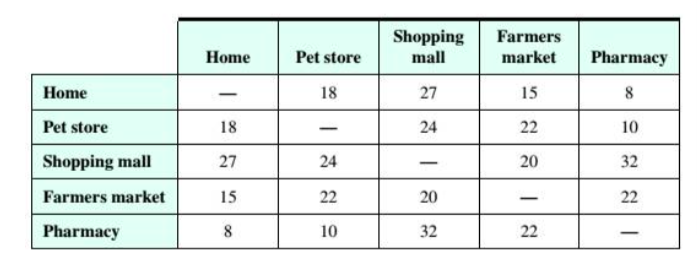
Route Planning Brian needs to visit the pet store, the shopping mall, the local farmers
market, and the pharmacy. His estimated driving times (in minutes) between the
locations are given in the table below. Use the greedy algorithm and the edge-picking
algorithm to find two possible routes, starting and ending at home, that will help
Brian minimize his total travel time

Shopping
mall
Farmers
Home
Pet store
market
Pharmacy
Home
18
27
15
8
-
Pet store
18
24
22
10
Shopping mall
27
24
20
32
-
Farmers market
15
22
20
22
-
Pharmacy
10
32
22
-

Expert Solution

This question has been solved!

Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.

This is a popular solution!

SEE SOLUTION Check out a sample Q&A here

Step 1

VIEW

Step 2

VIEW

Trending now

This is a popular solution!

Step by step

Solved in 2 steps with 1 images

SEE SOLUTION Check out a sample Q&A here

Knowledge Booster

$Paths and Circuits$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions

An insurance company hires an actuary to determine whether the number of hours of safety drivingclasses can be used to predict the number of driving accidents for each driver. Identify theexplanatory variable, if any.
find mean and sd of data 401,506,804,205,904,506,120,580,354,742,581,354,952
construct anova and show all calculation manually, thanks
A manufacturer inspects 400 personal video players and finds that 399 of them have no defects. The manufacturer sent a shipment of 1,600 personal video players to a distributor. Predict the number of players in the shipment that are likely to have no defects.
Create a boxplot for patient wait time for offices without a wait-tracking system
find first and third quartile 42,48,56,78,85,96,35,45,86,26,47,58,62,45,15,95,82,32,10,50,67,86,54,26,83
A group of 11 students from the same middle school have been asked to record how much time they spent this morning traveling from home to school. Here are the results (in minutes). Españal 6, 3, 15, 3, 5, 6, 4, 4, 11, 6, 4 Send data to calculator Find the median travel time for that group of students. |minutes Privacy Accessibility 02021 McGraw-Hill Education. All Rights Reserved Terms of Use MacBook Air
Use the average method to forecast enrollment in Spring 2022
Explain the Tukey HSD results in the attached table .
Guadalajara Tours' daily sightseeing trip has a capacity of 55 people. Each day, tour officials record the number of people making the trip. The data for a selection of 22 summer days are as follows. 31, 36, 41, 42, 43, 43, 46, 46, 46, 47, 47, 49, 51, 51, 51, 51, 52, 52, 52, 54, 54, 54 Send data to calculator Send data to Excel Frequency 10- 10 6+ 4 4. 2+ 1. 0- 30 35 40 45 50 55 Number of people on trip OMean (a) For these data, which measures of central tendency take more than one value? Choose all that apply. OMedian Mode ONone of these measures OMean (b) Suppose that the measurement 31 (the smallest measurement in the data set) were OMedian replaced by 15. Which measures of central OMode tondoncu would bo offoctod by the chano02 Explanation Check O 2021 McGraw-Hill Education. All Rights Reserved. Terms of Use Privacy Access APA pe here to search 99+
Write a short note on Tukey’s HSD test.
The GRE is a test required for admission to many U.S. graduate schools. Students' scores on the quantitative portion of the GRE follow a normal distribution with a min of 150 and a standard deviation of 8.8. An admissions officer at a large graduate school believes the mean is less than 150. What kind of test is this? Two-tailed Left-tailed Right-tailed