Complete the following proof. Given: WXYZ is a rectangle Prove: ZX = WY W. Statements Reasons 1. Given 1. WXYZ is a rectangle. 2. WXYZ is a parallelogram. 2. Definition of a rectangle 3. Opposite sides of a parallelogram are congruent. 3. WZ XY 4. ZWZY and 2XYZ are right angles. 4. Definition of a rectangle 5. All right angles are congruent. 5. 6. ZY = YZ 6. 7. AWZY÷AXYZ 7. SAS Triangle Congruence Theorem 8. ZX = WY 8. СРСТС
Complete the following proof. Given: WXYZ is a rectangle Prove: ZX = WY W. Statements Reasons 1. Given 1. WXYZ is a rectangle. 2. WXYZ is a parallelogram. 2. Definition of a rectangle 3. Opposite sides of a parallelogram are congruent. 3. WZ XY 4. ZWZY and 2XYZ are right angles. 4. Definition of a rectangle 5. All right angles are congruent. 5. 6. ZY = YZ 6. 7. AWZY÷AXYZ 7. SAS Triangle Congruence Theorem 8. ZX = WY 8. СРСТС
Elementary Geometry For College Students, 7e
7th Edition
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.
ChapterP: Preliminary Concepts
SectionP.CR: Review Exercises
Problem 36CR
Related questions
Question
Complete the following proof.
Given: WXYZ is a rectangle
Prove: ZY≅WY
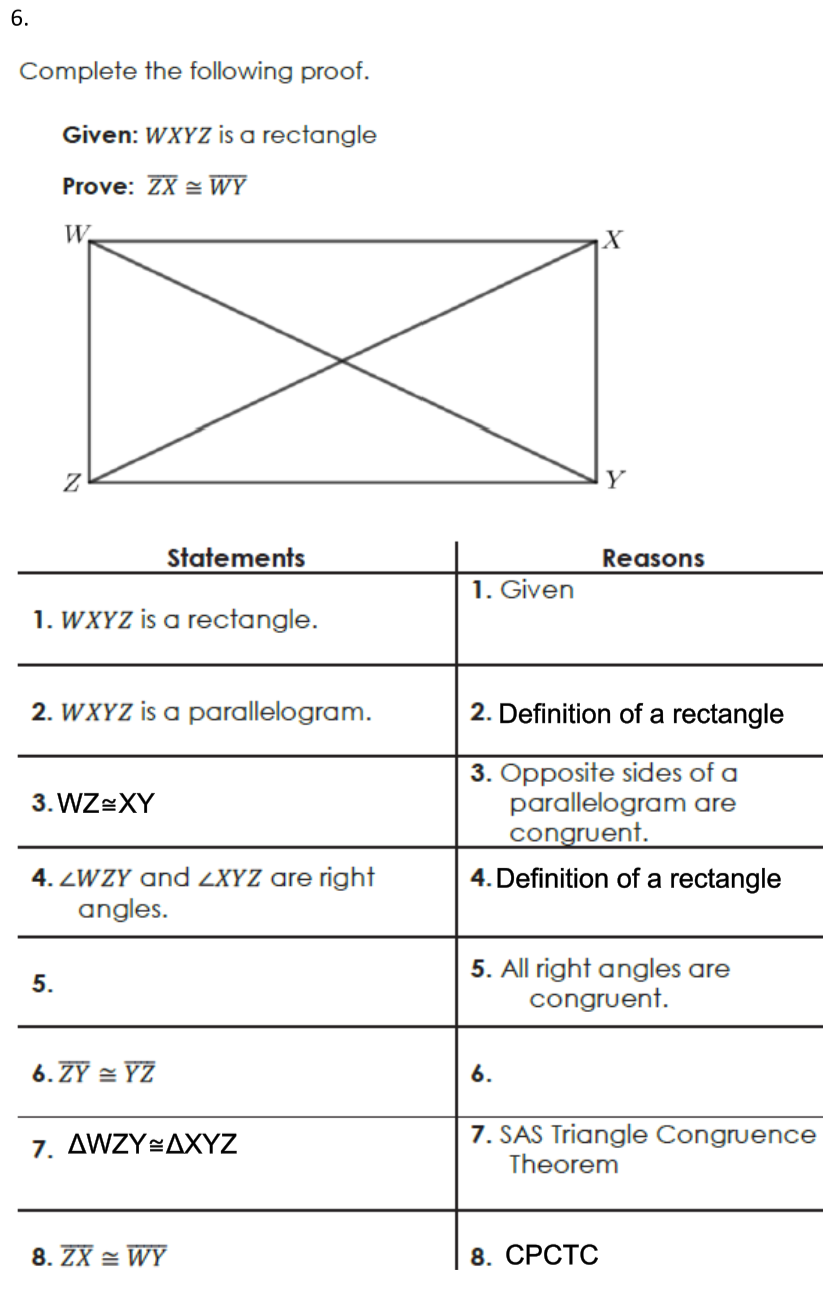
Transcribed Image Text:6.
Complete the following proof.
Given: WXYZ is a rectangle
Prove: ZX = WY
W.
X
Y
Statements
Reasons
1. Given
1. WXYZ is a rectangle.
2. WXYZ is a parallelogram.
2. Definition of a rectangle
3. Opposite sides of a
parallelogram are
congruent.
3. WZ=XY
4. Definition of a rectangle
4. ZWZY and 2XYZ are right
angles.
5. All right angles are
congruent.
5.
6. ZY = YZ
6.
7. AWZY÷AXYZ
7. SAS Triangle Congruence
Theorem
8. ZX = WY
8. СРСТС
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution!
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 2 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Recommended textbooks for you

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Elementary Geometry For College Students, 7e
Geometry
ISBN:
9781337614085
Author:
Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:
Cengage,

Elementary Geometry for College Students
Geometry
ISBN:
9781285195698
Author:
Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:
Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning