Answered: A right pyramid with square base is 32…

Elementary Geometry For College Students, 7e

7th Edition

ISBN:9781337614085

Author:Alexander, Daniel C.; Koeberlein, Geralyn M.

Publisher:Alexander, Daniel C.; Koeberlein, Geralyn M.

Chapter9: Surfaces And Solids

Section9.CR: Review Exercises

Problem 12CR

See similar textbooks

Related questions

Question

A right pyramid with square base is 32 cm high, if one side of the square base is 48cm, find the following: Area of its slant surface, Total surface area, Volume

Expert Solution

Step 1

It is given that, height h= 32 cm and the length of square side a = 48 cm.

Consider the right pyramid with square base shown below.

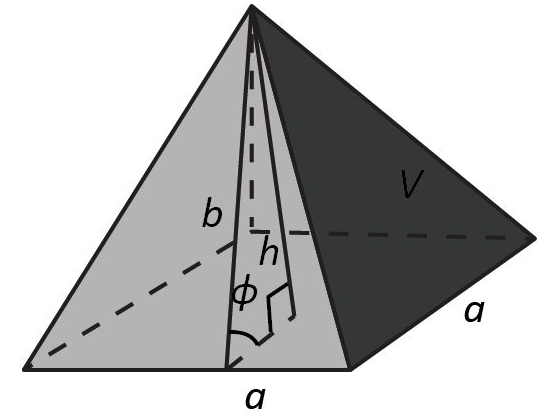
Step 2

(a) Obtain the area of slant surface as follows.

The expression for Area of slant surface is,

$\begin{array}{rcl} A & = & 4 \times Area of Triangle \\ = & 4 \times (\frac{a}{4} \times \sqrt{a^{2} + 4 h^{2}}) \\ = & 4 \times (\frac{48}{4} \times \sqrt{48^{2} + 4 {(32)}^{2}}) \\ = & 3840 {cm}^{2} \end{array}$

Therefore, Area of slant surface is 3840 cm²

Step by step

Solved in 4 steps with 1 images

Knowledge Booster

$Pyramids$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.

Similar questions