Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in terms of global or local range. The definition of minimization in the thesaurus is the process of reducing something to a small amount, value, or position. Minimization (noun) is an instance of belittling or disparagement.
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which one would be easier? Walking on the road would be much easier than climbing a mountain.
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the first derivative test and second derivative test to understand the concave behavior of the function.
A cylindrical metal can is to be made to hold 1 L of oil. Find the dimensions that will minimize the cost of the metal to manufacture the can. This condition will apply throughout the project. (1 Liter = 1000 cm3)
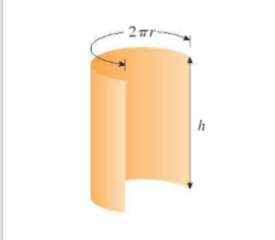
The material for cans is cut from sheets of metal. The cylindrical sides are formed by bending rectangles. These rectangles are cut from the sheet with little or no waste.
But if the top and bottom discs are cut from squares of side 2(see the figure on the left), this leaves considerable waste material, which may be recycled but has little or no value to the can makers. If this is the case, show that the amount of material used is minimized when (h/r)=(8/pi)= 2.55
Note: Start with the formula for the material required for one can- the lateral surface area + the area of 2 squares.
Part 1 – Write the formula for the value to be minimized and find the critical numbers.
Part 2 – Use the First or Second Derivative test to verify that a critical number will give us the minimum value.

Trending now
This is a popular solution!
Step by step
Solved in 4 steps with 3 images








