What is a Derivative?
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which one would be easier? Walking on the road would be much easier than climbing a mountain.
Of course, it is not about the distance because the distance is the same in both cases. The factor here is the steepness. Assume a person is climbing a mountain which is less steep and 500 meters high and another mountain which is much steeper and 450 meters high. He would find climbing a steeper mountain more difficult. The factor is not the height alone but the steepness. The steeper, the more difficult it will be to climb. The yellow lines in the below image represent the steepness of the mountains.
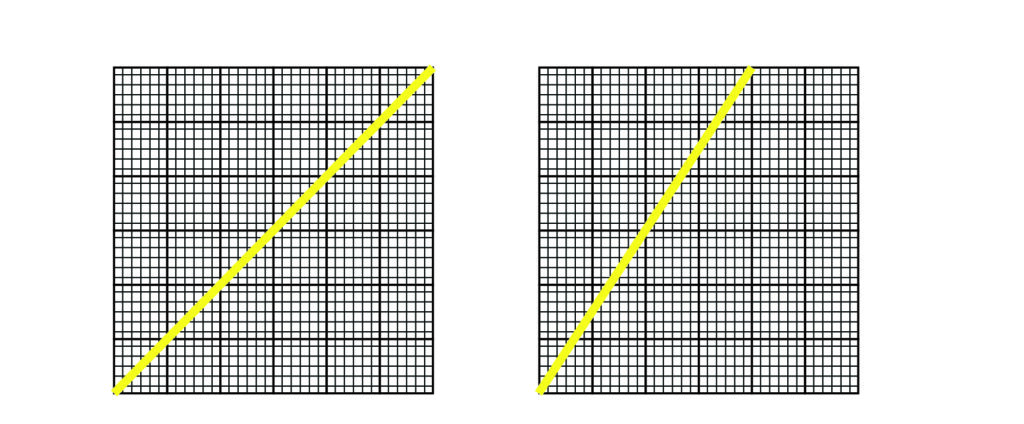
How to find the steepness and derivative related to this.
Slope
A slope is a number that helps in finding not only the steepness but also the direction of the line. The slope of the mountains is calculated by finding the ratio of distance covered by going upwards to the distance covered by going across.
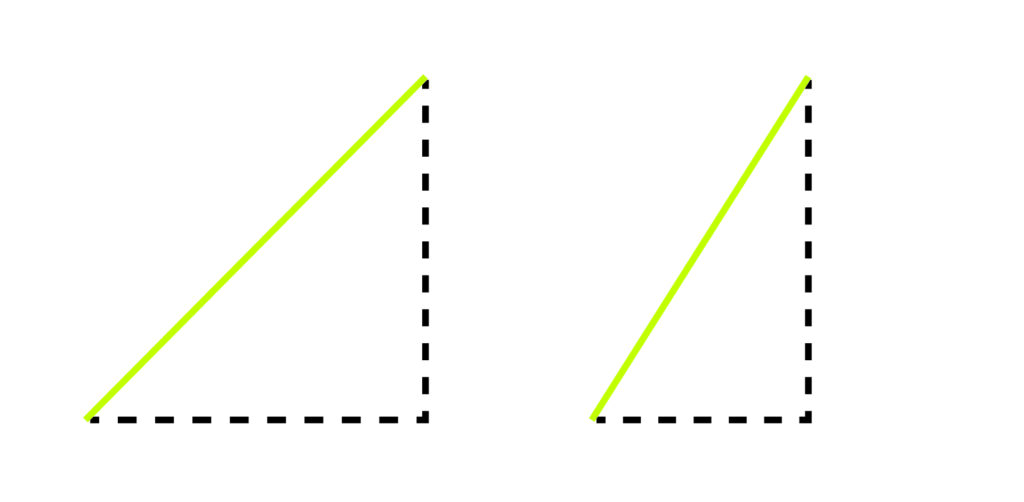
In other words, it is the ratio between the vertical length and the horizontal length. By drawing vertical and horizontal lines a triangle is obtained. The value gives an idea of how much vertical distance is covered in comparison to the horizontal distance. When the ratio is higher, the mountain will be steeper. The slope is also found by measuring the angle.
How to find the slope of a curve? This is where the concept of derivative and limit is used. A curve is represented algebraically as a function with two varying values.
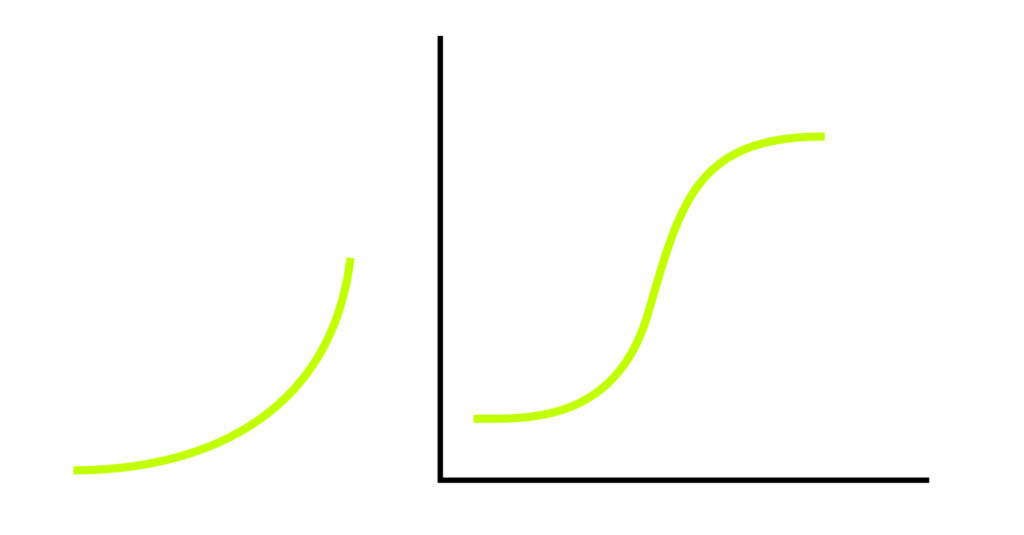
In the graph above, x values are given on the horizontal line and y=f(x) values on the vertical line. In a function, giving the input value as x, the result will be f(x)=y.
Write the elements in an ordered pair (x,y). This can be plotted in a graph. The variable y depends on x. As x keeps varying, y also keeps varying. Suppose that the value of x changes from an initial point x0 to x0+Δx which is a point at an infinitesimal distance from x. This means that adding Δx to x gives a value that is closer to x. Then f(x)=y also changes from the initial point f(x0)=y0 to f(x0)+f(x0+Δx)=y0+Δy, which is at an infinitesimal distance from x0.
The ratio shows how fast y is changing when compared to x. Take a curve. Plot a a point P on the curve.
The slope at point P is nothing but the ratio .
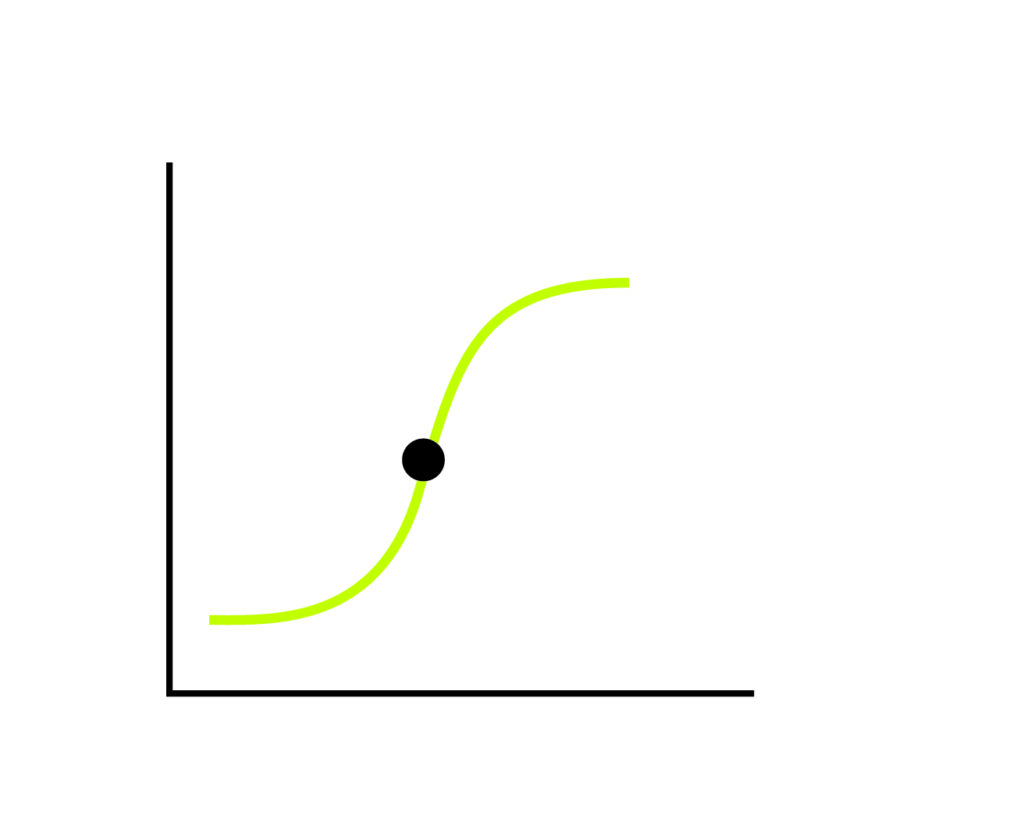
Take a small region around the point. Can the curve in that small region be seen as a straight line? The answer is yes. But how? From the earth, the moon appears to be round in shape. The astronaut steps on the moon like stepping on a flat surface. This is because, even though the moon is round in shape for a person watching from afar, for a person standing on a very small region on the moon it appears to be flat. In the same way, the small region of a curve with the point P is closer to a straight line. This straight line when extended is the tangent line at point P.
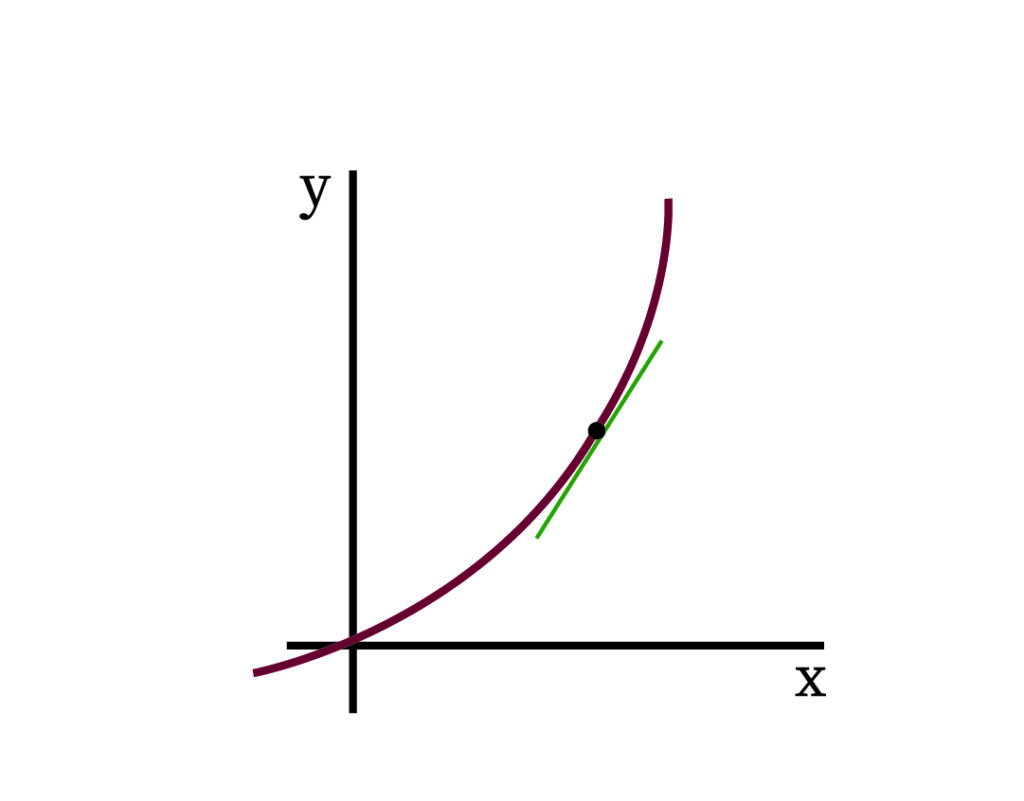
The slope changes depending on the point on the curve. If the point was somewhere else, the slope would also be different. This is the same way to calculate the speed of a vehicle. If x is the time taken to move from one place to another and y is the distance covered, the ratio of distance traveled to time shows how fast y is changing when we compare with x.
Representation of a Derivative
How to calculate the change at a point? Here comes the role of differentiation into action.
Calculate the time taken for traveling from point P to point Q.
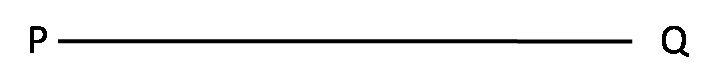
Consider that we started at P when the time was 12:00 noon and after reaching point Q the time is 12:02 pm. Therefore the time taken from P to Q is 2 minutes. x0 is the initial time and (x0+Δx) is the time after reaching Q. Therefore (x0+Δx)-x0=Δx and Δx=2. Now we have to calculate the distance traveled from P to Q. If f(x0) denotes the initial point P and f(x0+Δx) denotes the point Q, then the distance covered is the difference of f(x0) from f(x0+Δx). What will be the speed? We find the speed by calculating the ratio of distance traveled by the time taken.
The average speed=. Now join the points P and Q by a line.
The steepness of the line and the average speed are equal in the time interval
Δx between the same points on the curve.
We find the instantaneous speed from the average speed at small time intervals. Here we use the concept of limits.
For shorter time intervals we let Δx to go to zero.
So, when the , the average speed approaches the instantaneous speed.
As , the point Q comes near to the point P. The line joining P and Q is equal
to the line that touches the curve at the point P alone.
This is the process of differentiation. The instantaneous rate of change at y with respect to x at x0 is the derivative of the function at x0. This gives the formal definition of the derivative of a function.
The mathematical representation of a derivative is , where
.
Example
An example to have a better understanding of the derivatives.
If f(x) =8x, find at x=4.
Solution:
The derivative of 8x at x=4 is 8.
Formulas
Derivatives of Different Types of Functions
1. Derivative of constant
2. Derivative of the exponential function
3. Derivative of logarithmic functions
4. Derivatives of trigonometric functions
Basic Rules of Derivatives
If f and g are two differentiable functions, then the following rules are applicable:
- Sum rule
2. Difference rule
3. Product rule
4. Quotient rule
, if
5. Power rule
, , for real numbers n
6. Coefficient rule
7. Chain rule
Context and Applications
This topic is significant in the professional exams for both undergraduate and graduate courses, especially for
- Bachelor of Science Mathematics
- Master of Science Mathematics
Want more help with your calculus homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Derivatives Homework Questions from Fellow Students
Browse our recently answered Derivatives homework questions.