A cubical tank with a circular hole of area A, at the bottom has water leaking through it. Due to friction and contraction near the hole, the volume of water leaving the tank per second is reduced to cAn/2gh where c is an empirical constant with a range of values 0 < c< 1. Derive the differential equation for the height h of the remaining water at any time t. The radius of the hole is 50mm and g = 9.8.
A cubical tank with a circular hole of area A, at the bottom has water leaking through it. Due to friction and contraction near the hole, the volume of water leaving the tank per second is reduced to cAn/2gh where c is an empirical constant with a range of values 0 < c< 1. Derive the differential equation for the height h of the remaining water at any time t. The radius of the hole is 50mm and g = 9.8.
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Please box or circle the final answer. Thank You
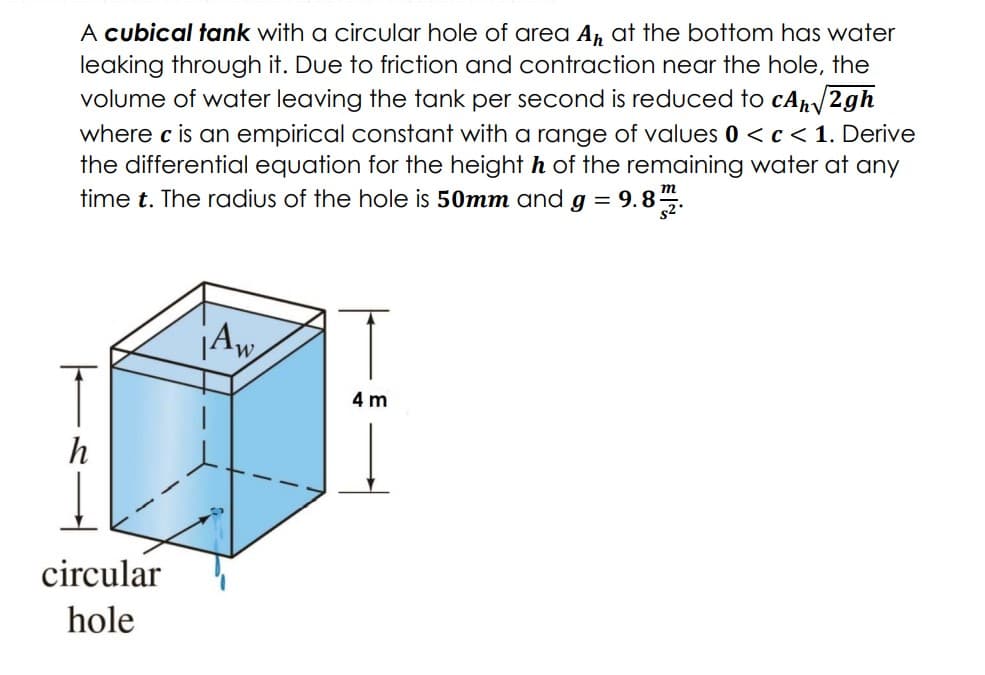
Transcribed Image Text:A cubical tank with a circular hole of area A, at the bottom has water
leaking through it. Due to friction and contraction near the hole, the
volume of water leaving the tank per second is reduced to cAp/2gh
where c is an empirical constant with a range of values 0 < c< 1. Derive
the differential equation for the height h of the remaining water at any
time t. The radius of the hole is 50mm and g = 9.85.
T
4 m
h
circular
hole
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 2 steps with 1 images

Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

