Explain the determine blue
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
Explain the determine blue
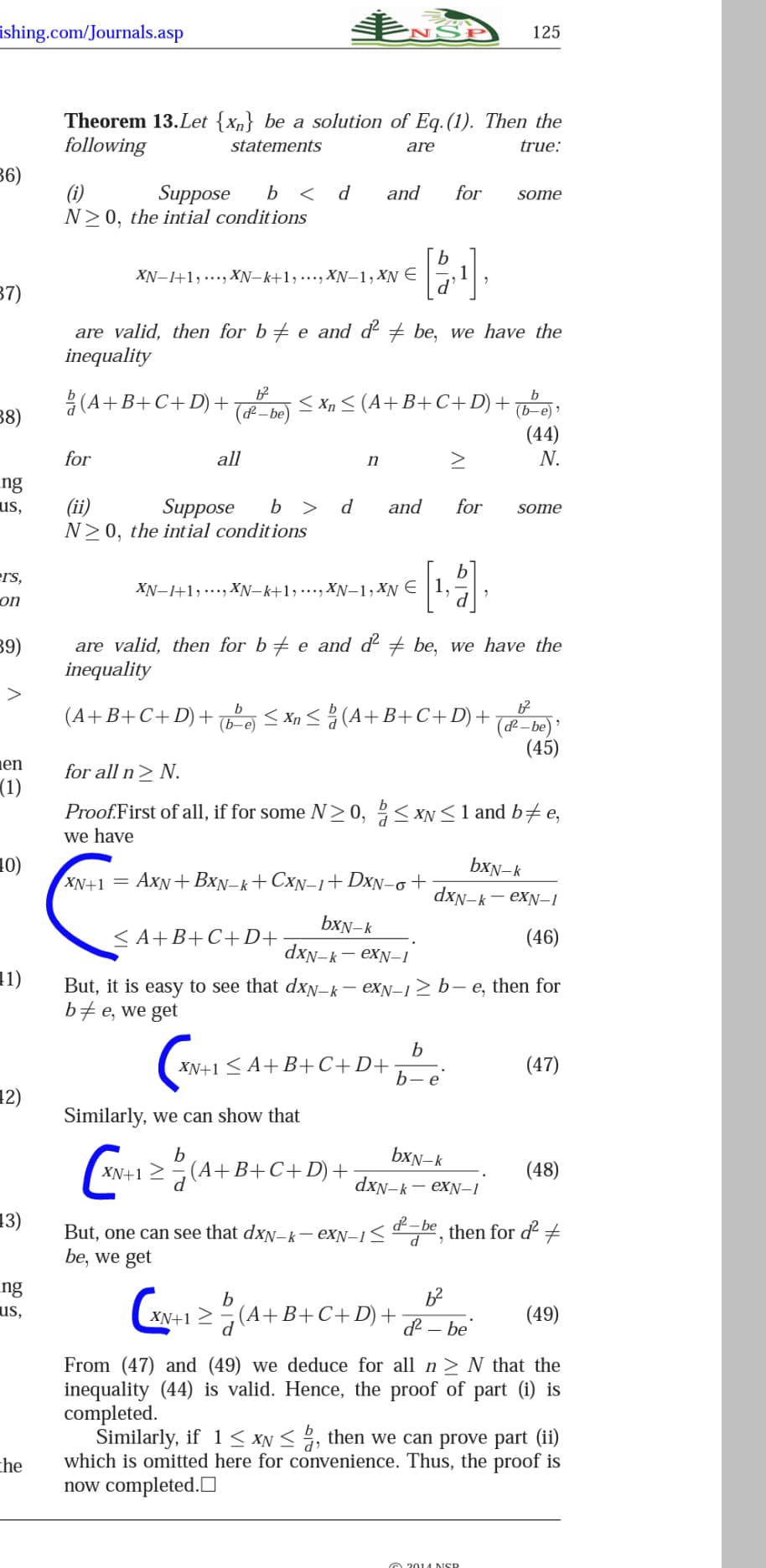
Transcribed Image Text:ishing.com/Journals.asp
125
Theorem 13.Let {xn} be a solution of Eq.(1). Then the
following
statements
are
true:
36)
b < d
(i)
N>0, the intial conditions
Suppose
and
for
some
XN-1+1,..., XN–k+1,……, XN-1, XN €
1
37)
are valid, then for b+ e and d² # be, we have the
inequality
(A+B+C+D) +
b
< Xn < (A+B+C+D)+
& – be)
(b-e) »
(44)
38)
for
all
n
N.
ng
us,
b > d
Suppose
N>0, the intial conditions
(ii)
and
for
some
ers,
XN-1+1, ..., хN-k+1,..., Xм-1, Xу €
1.
UO
39)
are valid, then for b+ e and d + be, we have the
inequality
>
b
(A+B+C+D)+o S Xn < (A+B+C+D)+
(df – be) '
(45)
(b-e)
en
for all n> N.
(1)
Proof.First of all, if for some N>0, 2< xN < 1 and b#e,
we have
10)
XN+1 = AxN+ BxN-k+CxN–i+DxN-o+
bxN-k
dxn-k– exN-1
bxN-k
< A+B+C+D+
(46)
dxN-k- exN-1
1)
But, it is easy to see that dxN-k– exN-12 b– e, then for
b#e, we get
b
XN+1 < A+B+C+D+
(47)
b-e'
12)
Similarly, we can show that
(w-1 2(A+ B+C+ D)-
b
bxN-k
XN+1 >
d
(48)
dxN-k — еxN-1
13)
&– be
then for d +
But, one can see that dxN-k– eXN–1<
be, we get
ng
us,
b
(A+B+C+D)+
XN+1 >
(49)
d – be
From (47) and (49) we deduce for all n> N that the
inequality (44) is valid. Hence, the proof of part (i) is
completed.
Similarly, if 1 < XN < , then we can prove part (ii)
which is omitted here for convenience. Thus, the proof is
now completed.O
che
A 201 4 NSP
AL
![The objective of this article is to investigate some
qualitative behavior of the solutions of the nonlinear
difference equation
bxn– k
X+1 = Axn+ Bxp–k+CXp-1+Dxp-o+
[dxn-k– ex-1
(1)
n= 0, 1,2, .....
where the coefficients A, B, C, D, b, d, e e (0,00), while
k, 1 and o are positive integers. The initial conditions
X-g,..., X_1,..., X_ k, ..., X_1, Xo are arbitrary positive real
numbers such that k < 1 < 0. Note that the special cases
of Eq. (1) have been studied in [1] when B= C= D= 0,
and k = 0,1= 1, b is replaced by
B=C= D=0, and k= 0, b is replaced by – b and in
[33] when B = C = D = 0, 1= 0 and in [32] when
A= C= D=0, 1=0, b is replaced by – b.
••..
- b and in [27] when
6.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F3e6fa233-173d-4c75-ac91-9f159b3c4543%2F4c3c8487-ccc9-4add-b0a5-f3d494953a4a%2Ftu6rcs_processed.jpeg&w=3840&q=75)
Transcribed Image Text:The objective of this article is to investigate some
qualitative behavior of the solutions of the nonlinear
difference equation
bxn– k
X+1 = Axn+ Bxp–k+CXp-1+Dxp-o+
[dxn-k– ex-1
(1)
n= 0, 1,2, .....
where the coefficients A, B, C, D, b, d, e e (0,00), while
k, 1 and o are positive integers. The initial conditions
X-g,..., X_1,..., X_ k, ..., X_1, Xo are arbitrary positive real
numbers such that k < 1 < 0. Note that the special cases
of Eq. (1) have been studied in [1] when B= C= D= 0,
and k = 0,1= 1, b is replaced by
B=C= D=0, and k= 0, b is replaced by – b and in
[33] when B = C = D = 0, 1= 0 and in [32] when
A= C= D=0, 1=0, b is replaced by – b.
••..
- b and in [27] when
6.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by step
Solved in 6 steps

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

