Homework Help is Here – Start Your Trial Now!
Math
Algebra
Find all the zeros of the polynomial function. Use the Rational Zero Theorem, Descartes's Rule of Signs, and possibly the graph of the polynomial function shown by a graphing utility as an aid in obtaining the first zero. fx)-x-3x-13x + 15 The zeros of the function are (Use a comma to separate your answers as needed.) Enter your answer in the answer box. P re to search hp HEW LETT PAC KAR D ins prt sc home 12 delete f11 10 f8 f4 & 7 $ 4 % 5 backspace O lock 9 6 3 } U T E R home enter L K H F D G pause Tshift M V B C ctrl alt 00

Find all the zeros of the polynomial function. Use the Rational Zero Theorem, Descartes's Rule of Signs, and possibly the graph of the polynomial function shown by a graphing utility as an aid in obtaining the first zero. fx)-x-3x-13x + 15 The zeros of the function are (Use a comma to separate your answers as needed.) Enter your answer in the answer box. P re to search hp HEW LETT PAC KAR D ins prt sc home 12 delete f11 10 f8 f4 & 7 $ 4 % 5 backspace O lock 9 6 3 } U T E R home enter L K H F D G pause Tshift M V B C ctrl alt 00

College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
12th Edition
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:R. David Gustafson, Jeff Hughes
Chapter4: Polynomial And Rational Functions
Section4.5: Zeros Of Polynomial Functions
Problem 79E
See similar textbooks
icon
Related questions
Question
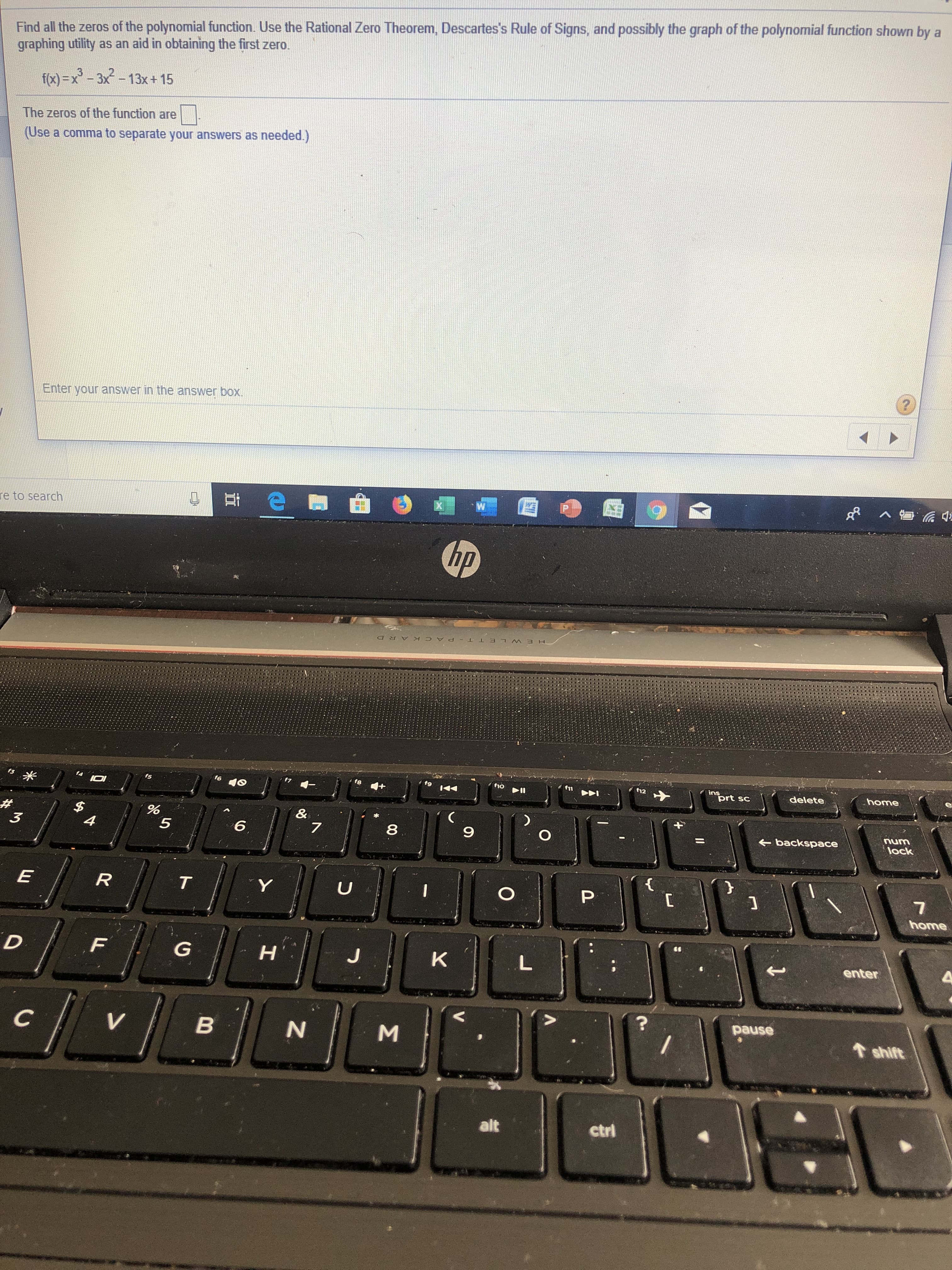
Find all the zeros of the polynomial function. Use the Rational Zero Theorem, Descartes's Rule of Signs, and possibly the graph of the polynomial function shown by a graphing utility as an aid in obtaining the first zero. fx)-x-3x-13x + 15 The zeros of the function are (Use a comma to separate your answers as needed.) Enter your answer in the answer box. P re to search hp HEW LETT PAC KAR D ins prt sc home 12 delete f11 10 f8 f4 & 7 $ 4 % 5 backspace O lock 9 6 3 } U T E R home enter L K H F D G pause Tshift M V B C ctrl alt 00
Transcribed Image Text:Find all the zeros of the polynomial function. Use the Rational Zero Theorem, Descartes's Rule of Signs, and possibly the graph of the polynomial function shown by a graphing utility as an aid in obtaining the first zero. fx)-x-3x-13x + 15 The zeros of the function are (Use a comma to separate your answers as needed.) Enter your answer in the answer box. P re to search hp HEW LETT PAC KAR D ins prt sc home 12 delete f11 10 f8 f4 & 7 $ 4 % 5 backspace O lock 9 6 3 } U T E R home enter L K H F D G pause Tshift M V B C ctrl alt 00
Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 8 steps with 6 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Recommended textbooks for you
College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:
9781305071742
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
College Algebra
College Algebra
Algebra
ISBN:
9781305115545
Author:
James Stewart, Lothar Redlin, Saleem Watson
Publisher:
Cengage Learning
College Algebra
College Algebra
Algebra
ISBN:
9781337282291
Author:
Ron Larson
Publisher:
Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry (MindTap Course List)
Trigonometry
ISBN:
9781337278461
Author:
Ron Larson
Publisher:
Cengage Learning
SEE MORE TEXTBOOKS